[Algorithm] Greedy Algorithm (탐욕 알고리즘)
Greedy Algorithm
A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. (위키피디아)
- 탐욕법 : 단계마다 최적의 선택을 하여 문제 해결을 수행하는 경험론적 알고리즘.
그리디 알고리즘은 이름에서 유추할 수 있듯이 각 단계마다 당장 가장 '좋은' 방법을 선택한다. 문제를 전체적으로 고려해 가장 좋은 것을 찾는 DP나 이진탐색과는 차이가 있다.
기본 접근법
- 선택 절차 (selection procedure)
특정 후보 중에 하나를 선택해 해당 방식이 주어진 문제의 해인지 결정하는 절차이다. 이때 해는 현재의 상황에서 가장 최선의 경우를 선택한다. - 타당성 조사(Feasibility check)
선택한 해가 과연 타당한 것인가에 대해 검사한다. - 해법 조사(solution check)
지금까지 선택한 해가 문제에서 요구하는 조건에 만족하는지 검사한다.
그리디 알고리즘의 장점은 굉장히 구현하기 좋다. 미래의 상황을 고려하지 않아도 되기 때문에 단순하면서도 강력한 방법이다. 하지만, 그리디 알고리즘은 적용할 수 있는 상황이 제한적이다. 그리디 알고리즘을 설명할 때 가장 먼저 나오는 예제인 동전 개수 문제를 예로 들어보자.
1, 5, 10, 20원짜리 동전이 있다. 동전을 가장 적게 사용하여 36원을 딱 맞춰 지불하려고 할 때, 몇 개의 동전을 사용해야할까?
위 문제를 딱 보면 누구나 쉽게 해답을 찾을 수 있다.
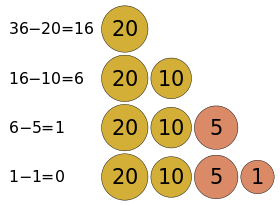
1. 20원 동전을 최대로 사용한다. => 1개를 사용하고 16원이 남는다.
2. 10원 동전을 최대로 사용한다. => 1개를 사용하고 6원이 남는다.
3. 5원 동전을 최대로 사용한다. => 1개를 사용하고 1원이 남는다.
4. 1원 동전으로 남은 돈을 모두 지불한다. => 1개를 사용한다.
위의 순서를 거쳐 총 4개의 동전을 주면 된다.
우리는 그냥 현재 상황에서 사용할 수 있는 가장 높은 가격의 동전을 사용했다. 그리고 놀랍게도 이것이 실제 그리디 알고리즘을 이용해 푼 방법과 동일하며 정답에 해당한다. 이 방법은 그리디 알고리즘이라는 용어를 모르는 사람도 충분히 생각할 수 있다. 즉, 그리디 알고리즘은 굉장히 직관적이고 합리적인 알고리즘이다.
https://www.acmicpc.net/problem/11047
11047번: 동전 0
첫째 줄에 N과 K가 주어진다. (1 ≤ N ≤ 10, 1 ≤ K ≤ 100,000,000) 둘째 줄부터 N개의 줄에 동전의 가치 Ai가 오름차순으로 주어진다. (1 ≤ Ai ≤ 1,000,000, A1 = 1, i ≥ 2인 경우에 Ai는 Ai-1의 배수)
www.acmicpc.net
이 문제가 그리디를 적용할 수 있는 동전 문제이다.
그럼, 이 알고리즘을 모든 경우에 적용할 수 있을까? 예상했겠지만 당연히 아니다. 위의 동전개수 문제를 변형해보겠다.
1, 6, 7원짜리 동전이 있다. 동전을 가장 적게 사용하여 12원을 지불하려고 할 때, 몇 개의 동전을 사용해야할까?
그리디를 적용하여 문제를 해결해보자.
1. 7원 동전을 최대로 사용한다. => 1개를 사용하고 5원이 남는다.
2. 6원 동전을 최대로 사용한다. => 0개를 사용하고 5원이 남는다.
3. 1원 동전을 최대로 사용한다. => 5개를 사용한다.
이렇게 총 6개를 사용하는 방법이 나온다. 하지만, 이것이 정답인가? 아니다. 6원 동전 2개를 내면 12원이 완성되기 때문이다. 실제로 동전 문제는 각 동전 단위가 배수 관계에 있어야지만 greedy를 이용해 해결할 수 있다.
그리디는 강력하고 구현하기 쉽지만, 그 결과가 진짜 최적의 경우인지 판단를 할 필요가 있으며, 복잡한 경우에는 그것을 알아내기가 어렵다. 때론 구현의 난이도를 낮추기 위해 그리디를 적용하는 경우도 있지만, 이는 일부 손해를 감수하고 사용하는 경우일 때도 있다.
대표적으로 그리디 알고리즘을 적용할 수 있다고 알려진 예시들이 있다.
- Activity selection (활동 선택)
- Job scheduling (잡 스케쥴링)
- Huffman Coding (허프만 코딩)
- Shortest path problem (최단 경로 문제)
오늘은 일단 활동 선택 문제에 대해서만 알아보고 나머지 내용은 따로 글을 올리겠다.
2023.06.08 - [Computer Science/Data structure & Algorithm] - [Algorithm] Huffman code (허프만 코드)
[Algorithm] Huffman code (허프만 코드)
허프만 코드는 그리디 알고리즘으로 해결할 수 있는 대표적인 문제이다. 오늘은 허프만 코드가 무엇인지, 그리고 어떻게 구현하는지에 대해 알아볼 것이다. 2023.06.08 - [Computer Science/Data structure &
mobuk.tistory.com
활동 선택 문제 (Activity Selection Problem)
문제 상황
여러 개의 활동이 있을 때, 가장 많은 활동을 처리할 수 있는 스케줄을 짜는 문제. 각 활동은 시작시간과 종료시간이 주어져 있으며, 한번에 하나만 해결할 수 있다.
- 자원을 사용하기 원하는 활동들 : A = { a1, a2, ... an }
- 각 활동의 시작시간 S = {s1, s2, ... sn }
- 각 활동의 종료시간 F = {f1, f2, ... fn}
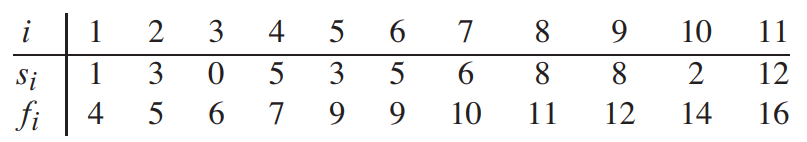
- fi > sj 일 경우 sj는 실행되지 못한다. ( = 두 활동을 동시에 할 수 없다. = 진행 중인 활동이 종료된 뒤 시작해야한다.)
- 활동들은 끝나는 시간을 기준으로 정렬되어 있다.
해결 방법
- 가장 먼저 끝나는 활동을 선택
- 이전에 선택한 활동과 겹치지 않는 활동 중 가장 먼저 끝나는 활동을 선택함.
- 선택한 활동들의 목록을 반환함.
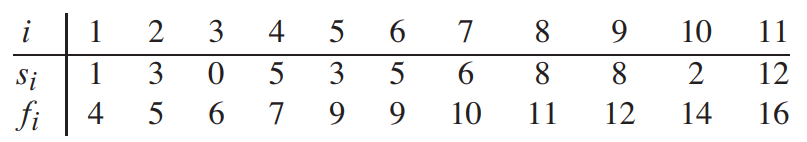
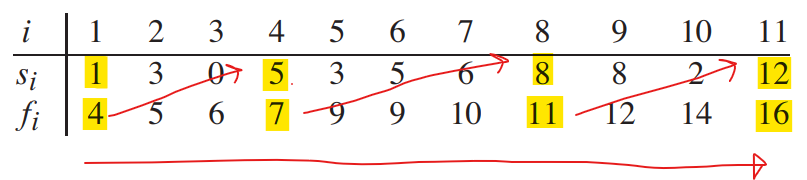
위 예제를 참고하여 풀어나가면 아래와 같다.
1) 가장 먼저 끝나는 활동 1번을 선택한다 (1~4)
2) 시작 시간이 4보다 큰 것들 중 가장 먼저 끝나는 활동을 선택한다. = 활동 4번 (5~7)
3) 시작 시간이 7보다 큰 것들 중 가장 먼저 끝나는 활동을 선택한다. = 활동 8번 (8~11)
4) 시작 시간이 11보다 큰 것 중 가장 먼저 끝나는 활동을 선택한다. = 활동 11번 (12 ~16)
5) 시작 시간이 16보다 큰 것은 없기에 (배열의 끝에 도달) 최종 결과는 a1, a4, a8, a11이다.
슈도 코드로 나타내면 아래와 같다.
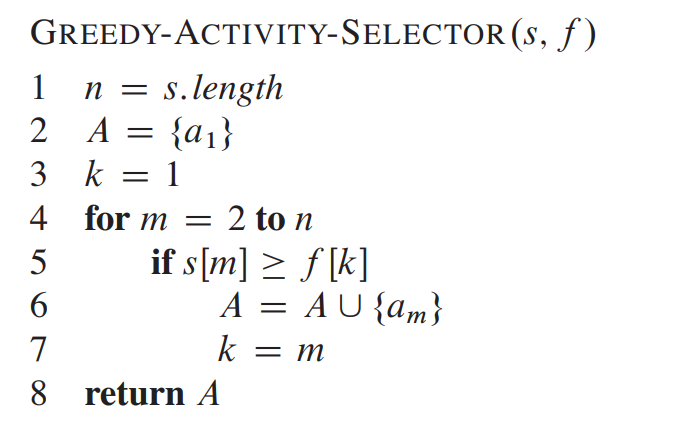
우리는 이 문제를 DP 로도 해결 할 수 있다.


하지만, 작동 과정을 보면 불필요한 부분까지 재귀로 살펴보아야 하기 때문에(모든 부분 문제를 풀어봐야해서) 비효율적이라는 것을 알 수 있다.
이처럼 그리디 알고리즘이 잘 적용되는 경우에는 불필요한 탐색 시간을 줄이고 각 단계에서 최적의 선택을 할 수 있다.
https://www.acmicpc.net/problem/1931
1931번: 회의실 배정
(1,4), (5,7), (8,11), (12,14) 를 이용할 수 있다.
www.acmicpc.net
위 과정을 이해했다면 위 문제를 충분히 해결할 수 있을 것이다.
'Computer Science > Data structure & Algorithm' 카테고리의 다른 글
| [Algorithm] Dijkstra's Algorithm ( 다익스트라 알고리즘 ) (2) | 2023.06.10 |
|---|---|
| [Algorithm] Huffman code (허프만 코드) (0) | 2023.06.08 |
| [Algorithm] Knapsack algorithm - Greedy 사용 (0) | 2023.06.08 |
| [Algorithm] Knapsack algorithm (배낭 알고리즘) - DP 이용 (0) | 2023.06.07 |
| [algorithm] Floyd-Warchall algorithm (0) | 2023.05.24 |













