[Algorithm] Huffman code (허프만 코드)
허프만 코드는 그리디 알고리즘으로 해결할 수 있는 대표적인 문제이다. 오늘은 허프만 코드가 무엇인지, 그리고 어떻게 구현하는지에 대해 알아볼 것이다.
2023.06.08 - [Computer Science/Data structure & Algorithm] - [Algorithm] Greedy Algorithm (탐욕 알고리즘)
[Algorithm] Greedy Algorithm (탐욕 알고리즘)
Greedy Algorithm A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. (위키피디아) 탐욕법 : 단계마다 최적의 선택을 하여 문제 해결을 수행하는 경험
mobuk.tistory.com
그리디에 대해 알고 싶다면 위 글을 참고하길 바란다.
Huffman code
허프만 코드(Huffman code)는 문자를 코드화 시키는 과정에서 사용한다. 자주 사용되는 문자는 적은 비트로 된 코드로 변환하고 별로 사용하지 않는 문자는 많은 비트로 된 코드로 변환하여 전체 데이터를 표현하는 데 필요한 비트의 양을 줄이는 방법이다. 그래서 현대에서는 대부분의 문서 압축 프로그램에서 사용하는 방법이다.

위의 표를 보면 Fixed-length codeword는 3bit로 동일하다. 하지만, Variable-length codeword는 빈도수가 제일 높은 a는 1bit, 빈도수가 낮은 f는 4bit를 사용한다.
위의 비율을 가진 100,000 자의 문장이 있다고 했을 때, fixed-length는 300,000bit(100,000*3)이다. 하지만, 가변 길이인 것은 총 224,000 ((1 * 45 + 3 * 13 + 12 * 3 + 16 * 3 + 9 * 4 + 5 * 4 ) * 1,000 ) bit이다. 이 파일을 약 25% 효율적으로 코드 변환을 한 것을 알 수 있다.
그럼 직접 부호화를 시켜보자. 간단하게 가장 많이 나오는 수부터 차례대로 0, 10, 11, 100 .. 순으로 붙이면 될까?
당연히 그러면 안된다는 것이 질문에 대한 답이다.
어떤 문자열의 코드 길이가 고정되어 있다면 그 길이만큼 끊어서 읽으면 된다. 하지만, 그렇지 않은 경우, 우리는 어디까지가 그 문자열을 의미하는지 알 수 없다. 예를 한번 보자.
code : 010010
A = 0, B = 1, C = 10, D = 11
과연 위 코드는 0 - 1 - 0 - 0 -1 - 0 (ABABAB) 일까? 아니면 0 - 10 - 1 - 0 - 1 (ACBAB) 일까? 아니면 그 외 다른 것일까? 우리가 구분하지 못하는 것처럼 길이를 알지 못하면 우리는 이것이 무엇을 의미하는지 모른다. 우리는 이 상황을 Prefix codes를 만들어 해결할 것이다.
Prefix codes
어떤 문자열의 코드가 다른 문자열의 코드의 접두사(prefix) 가 되지 않는 유형의 코드. 즉, 어떤 코드도 다른 코드의 시작 부분이 되지 않게 만드는 코드이다.
code : 010010
A = 0, B = 10, C = 110, D = 111
이렇게 되면 위 코드는 0 - 10 - 0 - 10 으로 ABAB가 된다는 것이 명확해진다. 네 알파벳을 잘 보면 각 코드가 다른 문자열의 접두사가 되지 않는다. A를 예시로 들면 A가 0이기 때문에 다른 문자들은 0으로 시작할 수 없다. 0으로 시작하면 A인지 다른 문자의 시작부분인지 알 수 없기 때문이다.
보통 Prefix code를 만들 때 이진 트리를 사용한다. 이진트리에서 왼쪽 child로 이동하는 것을 0, 오른쪽 child로 이동하는 것을 1로 표현한다.
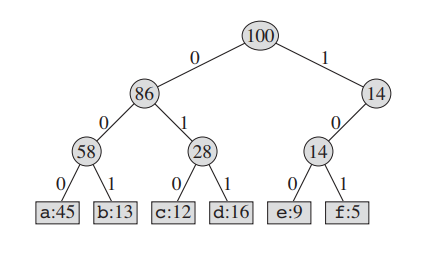
위의 full binary tree가 있다고 가정하자. a : 000 b : 001 c : 010 d : 011 e : 100, f : 101이 된다. 이렇게 되면 fixed-length codeword 가 되는 모습을 볼 수 있다.
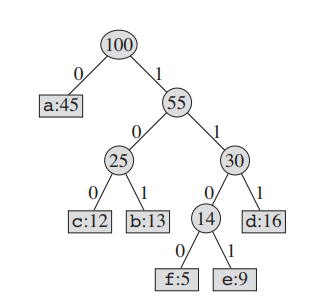
이번 트리는 huffman code를 나타낼 수 있는 tree 구조이다. a : 0 b : 101 c : 100 : d : 111 : e : 1101 : f 1100 이다. 이런 트리 구조를 어떻게 구현이 되었을까?
Huffman code 구현
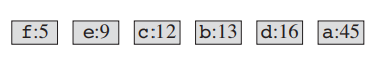
1. 데이터에서 사용되는 각 문자에 대한 출현 빈도수를 구한다. 그 뒤 빈도수를 기준으로 내림차순 정렬을 한다.
| 문자 | a | b | c | d | e | f |
| 빈도수 | 45 | 13 | 12 | 16 | 9 | 5 |
2. 출현 빈도가 가장 적은 2개의 문자를 child로 연결한다. parent는 두 문자의 빈도수의 합이다.
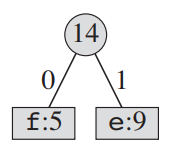
3. 그 뒤 parent의 빈도수와 다른 문자들의 빈도수를 정렬한다.
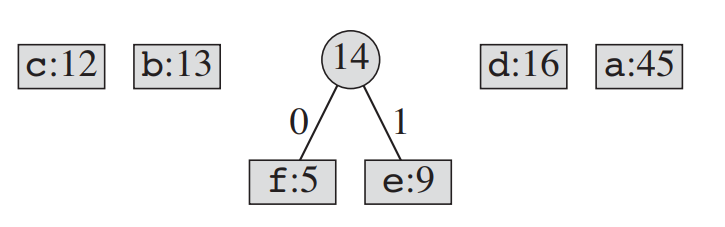
2~3의 과정을 반복한다.
[두 번째 cycle]
- 출현빈도가 가장 낮은 2개의 문자를 child로 연결한다. (2번 과정)
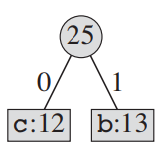
- 재정렬한다.
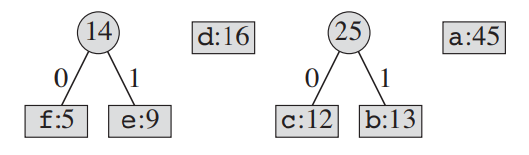
[세 번째 cycle]
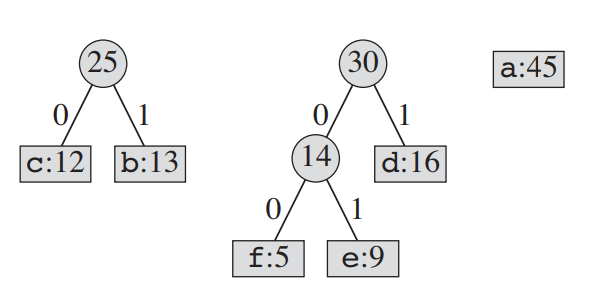
[네 번째 cycle]
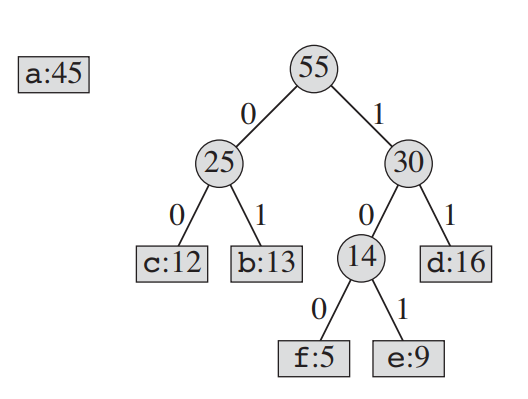
[다섯 번째 cycle]
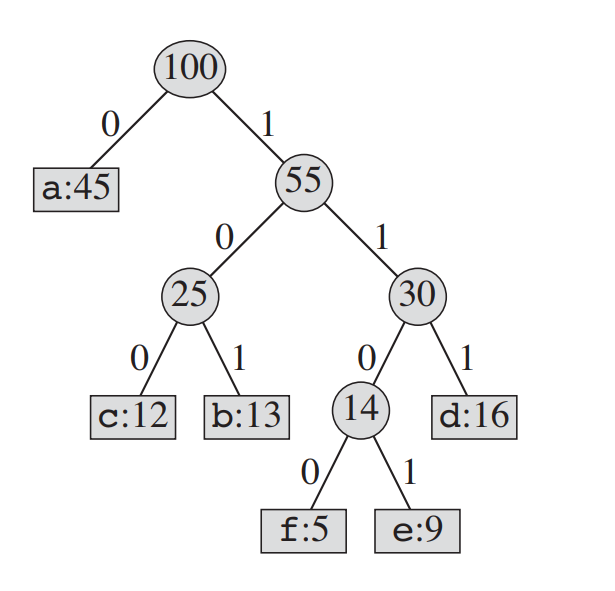
모든 노드를 연결되었다. 이 과정을 슈도 코드로 나타내면 아래와 같다.

Queue를 하나 선언해주고 Queue에 (문자, 빈도수) 를 넣어준다. 큐에서 가장 작은 값 2개를 빼서 각각의 빈도수를 root로 하는 트리를 만들어 준다. 그리고 다시 큐에 넣는다. 이 것을 queue에 들어있는 원소 개수 -1 번 만큼 반복하고 root 를 return 하면 된다.
Huffman code의 cost
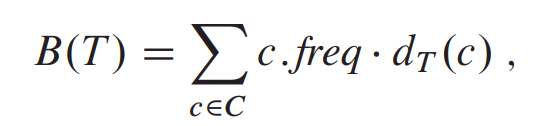
dT(c)는 character c의 codeword 길이를 의미한다.
'Computer Science > Data structure & Algorithm' 카테고리의 다른 글
| [자료구조] Graph (0) | 2023.06.12 |
|---|---|
| [Algorithm] Dijkstra's Algorithm ( 다익스트라 알고리즘 ) (2) | 2023.06.10 |
| [Algorithm] Greedy Algorithm (탐욕 알고리즘) (0) | 2023.06.08 |
| [Algorithm] Knapsack algorithm - Greedy 사용 (0) | 2023.06.08 |
| [Algorithm] Knapsack algorithm (배낭 알고리즘) - DP 이용 (0) | 2023.06.07 |













