[Algorithm] Greedy - Scheduling
그리디 알고리즘에 해당하는 Scheduling 문제들에 대해 정리해보았다.
Job Scheduling 문제는 크게 3가지 유형이 있다.
- Interval Scheduling
- Interval Partitioning
- Scheduling to Minimize Lateness
Interval Scheduling
시작시간과 종료시간이 존재하는 job이 여러 개 있을 때 시간이 겹치는 job은 overlab될 수 없다. 이 때 최대로 실행할 수 있는 job subset을 구하는 문제이다.
이 문제에 대해서는 Greedy 알고리즘을 소개하면서 '활동 선택 문제' 라고 해서 설명한 적이 있다. 그렇기 때문에 아래 글을 참고하길 바란다.
2023.06.08 - [Computer Science/Data structure & Algorithm] - [Algorithm] Greedy Algorithm (탐욕 알고리즘)
[Algorithm] Greedy Algorithm (탐욕 알고리즘)
Greedy Algorithm A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. (위키피디아) 탐욕법 : 단계마다 최적의 선택을 하여 문제 해결을 수행하는 경험
mobuk.tistory.com
Interval Partitioning
시작 시각과 종료 시각이 존재하는 job이 여러개 있고 그것을 실행할 수 있는 room이 여러 개 있을 때 최소한의 방을 사용해 모든 job을 실행할 수 있도록 scheduling 하는 방법 찾기
Interval Scheduling은 finish time을 기준으로 나열한다. Interval paritioning 은 start time을 기준으로 정렬한다.
과정
- 모든 interval을 start time 기준으로 정렬한다.
- start time이 가장 낮은 interval을 고른다. ( 선택되지 않은 것 중)
- 여러개의 방 중 free 상태가 가장 길었던 방에 넣는다.( 만약 되는 방이 없으면 새로운 방을 만든다. )
- 2 ~3을 모든 interval이 반영될 때 까지 반복한다.
예제 풀이
새로운 예제를 챙겨오는거 보다 백준 문제를 보여주면 편할 것 같아서 백준 문제를 들고왔다.
https://www.acmicpc.net/problem/1374
1374번: 강의실
첫째 줄에 강의의 개수 N(1 ≤ N ≤ 100,000)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 줄마다 세 개의 정수가 주어지는데, 순서대로 강의 번호, 강의 시작 시간, 강의 종료 시간을 의미한다. 강의
www.acmicpc.net
문제
N개의 강의가 있다. 우리는 모든 강의의 시작하는 시간과 끝나는 시간을 알고 있다. 이때, 우리는 최대한 적은 수의 강의실을 사용하여 모든 강의가 이루어지게 하고 싶다.
물론, 한 강의실에서는 동시에 2개 이상의 강의를 진행할 수 없고, 한 강의의 종료시간과 다른 강의의 시작시간이 겹치는 것은 상관없다. 필요한 최소 강의실의 수를 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 강의의 개수 N(1 ≤ N ≤ 100,000)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 줄마다 세 개의 정수가 주어지는데, 순서대로 강의 번호, 강의 시작 시간, 강의 종료 시간을 의미한다. 강의 번호는 1부터 N까지 붙어 있으며, 입력에서 꼭 순서대로 주어지지 않을 수 있으나 한 번씩만 주어진다. 강의 시작 시간과 강의 종료 시간은 0 이상 10억 이하의 정수이고, 시작 시간은 종료 시간보다 작다.
출력
첫째 줄에 필요한 최소 강의실 개수를 출력한다.
예제 입력 1
8
6 15 21
7 20 25
1 3 8
3 2 14
8 6 27
2 7 13
4 12 18
5 6 20
예제 출력 1
5
풀이
한 가지 key 포인트는 강의실 중 free시간이 가장 긴 것 (즉 이전 finish time이 가장 빠른 곳) 을 찾을 때 우선순위 큐를 사용하는 것이다.
import heapq
import sys
input = sys.stdin.readline
pq = []
ans = []
arr = []
N = int(input())
pq = []
for i in range(N):
n, s, f = map(int, input().split())
arr.append([s, f])
arr.sort()
heapq.heappush(pq, arr[0][1])
for i in range(1, N):
if pq[0] > arr[i][0]:
heapq.heappush(pq,arr[i][1])
else:
heapq.heappop(pq)
heapq.heappush(pq,arr[i][1])
print(len(pq))
Scheduling to minimize Lateness
length와 deadline을 가지는 job이 여러 개 있고 한 시점에 하나의 job 밖에 실행되지 못한다고 한다. lateness는 finish time - deadline을 의미하며 최대 lateness의 크기를 최소화 하는 문제이다.
아이디어는 "마감기한이 빠른 것" 순서대로 하는 것이다.
과정
- 마감기한이 빠른 순서대로 정렬한다.
예제 풀이
- 문제 상황
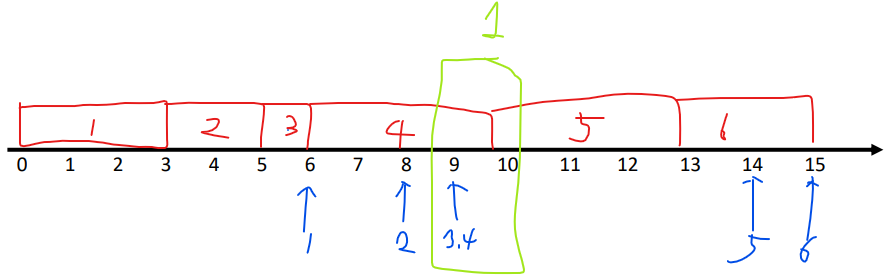
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Tj | 3 | 2 | 1 | 4 | 3 | 2 |
| Dj | 6 | 8 | 9 | 9 | 14 | 15 |
(이미 D를 기준으로 정렬되어 있다.)
그런다음 순서대로 블럭 밀어넣듯이 넣으면 된다.
'Computer Science > Data structure & Algorithm' 카테고리의 다른 글
| [Algorithm] Shell Sort (2) | 2023.10.13 |
|---|---|
| [Algorithm] Union Find (1) | 2023.09.16 |
| [Algorithm] Minimum Spanning Tree - Prim (0) | 2023.06.13 |
| [Algorithm] Minimum Spanning Tree - Kruskals (0) | 2023.06.13 |
| [Algorithm] Strongly Connected Components (강한 연결 요소) (1) | 2023.06.13 |













