[Algorithm] Minimum Spanning Tree - Kruskals
Spanning Tree
Spanning Tree는 어떤 그래프의 정점을 모두 포함한 가장 작은 subgraph를 의미한다.
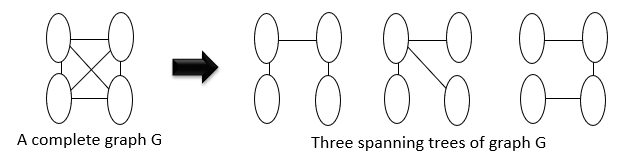
spanning tree를 찾는 가장 쉬운 방법은 DFS와 BFS를 이용하는 것이다.

2023.06.13 - [Computer Science/Data structure & Algorithm] - [Algorithm] BFS, DFS
[Algorithm] BFS, DFS
그래프를 탐색하는 대표적인 방식에는 BFS와 DFS가 있다. 그래프 관련 알고리즘, 동적 프로그래밍 등 다양한 알고리즘 과정에서 응용된 형태로 많이 사용하기 때문에 알고리즘 공부를 할 때에는
mobuk.tistory.com
Minimum Spanning tree

모든 정점 사이의 비용 (weight) 이 있다고 해보자. 우리는 spanning tree 중 가장 작은 비용이 드는 것을 찾고 싶다. 그런 spanning tree를 Minimum Spanning Tree(MST)라고 한다. 이 때도 bfs와 dfs 를 사용하면 해결 할 수 있을까?
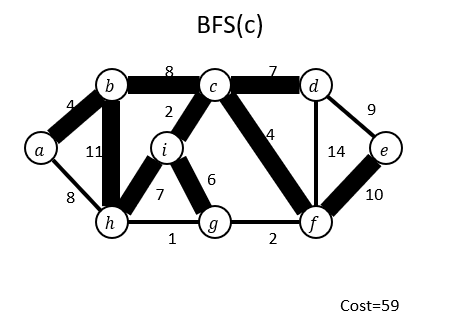

위 사진을 보면 BFS, DFS로 해결할 수 없다는 것을 알 수 있다. 우연하게 결과가 같을 수는 있지만, 결국 이건 모든 상황에서 적용할 수 없다.
Minimum Spanning Tree를 구하는 대표적인 알고리즘이 여러개 있다.
- Kruskal's algorithm
- Prim's algorithm
- Sollin's algorithm
오늘은 이 중 Kruskal's algorithm을 알아볼 것이다.
Kruskal's algorithm
교수님께서 1학년 때 kruskal과 prim 알고리즘을 소개해주시면서 kruskal은 prim보다 사람이 이해하기에는 편하지만, 구현 난이도가 높다고 하셨다. 그만큼 개념 자체는 간단하니 쉽게 이해할 수 있을 것이다.
과정
- 간선의 비용이 낮은 것부터 하나씩 MST에 포함시킨다.
- 선택한 간선이 cycle을 만든다면 그냥 넘어간다. ( MST에 포함시키지 않는다. )
- 모든 간선을 고려할 때 까지 1, 2를 반복한다.
예제 풀이
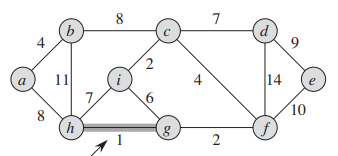
가장 간선의 비용이 낮은 h-g를 선택한다.
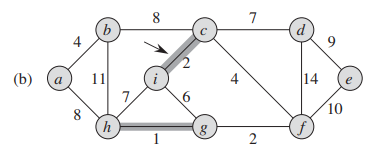
그 다음 간선의 비용이 낮은 i-c를 선택한다.
같은 방식으로 계속 선택해나간다.
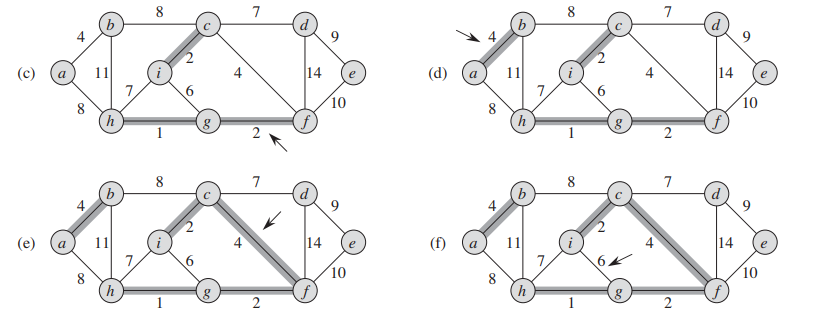
위 사진의 마지막 경우를 보자. i-g를 선택하려고 했는데 cycle이 생긴다. 그러면 그냥 넘어간다. 이런 방식으로 끝까지 진행하면 된다.


이렇게 쉽게 찾을 수 있다. 이 과정을 슈도 코드로 나타내면 아래와 같다.

코드를 보면 왜 구현 난이도가 높다는지 알 수 있다. 우선, cycle이 어떻게 생성되는지는 어떻게 판별할 수 있을까? 이런 것들이 코드를 어렵게 만든다.
시간복잡도 : O(E lg(E))
'Computer Science > Data structure & Algorithm' 카테고리의 다른 글
| [Algorithm] Greedy - Scheduling (0) | 2023.06.13 |
|---|---|
| [Algorithm] Minimum Spanning Tree - Prim (0) | 2023.06.13 |
| [Algorithm] Strongly Connected Components (강한 연결 요소) (1) | 2023.06.13 |
| [Algorithm] BFS, DFS (0) | 2023.06.13 |
| [자료구조] Graph (0) | 2023.06.12 |













