[AI] Support Vector Machine (SVM) - Linear

이번 파트는 수식이 좀 많다보니 직접 타이핑 한 것 보다 필기자료를 들고 오는게 나을 것 같아서 글보다 비교적 사진이 많을 예정이다.
 

Support Vector Machine 

SVM은 기계 학습 분야 중 하나로 패턴인식, 자료 분석을 위한 지도학습 모델이다. Classification, Regression에 사용할 수 있다. 
일단, Classification에 초점을 두고 SVM을 알아보자. 데이터를 두 부류로 분리할 때 여백을 최대로 가지는 초평면(hyperplane)을 찾는 것이 이 모델의 최종 목표이다. 

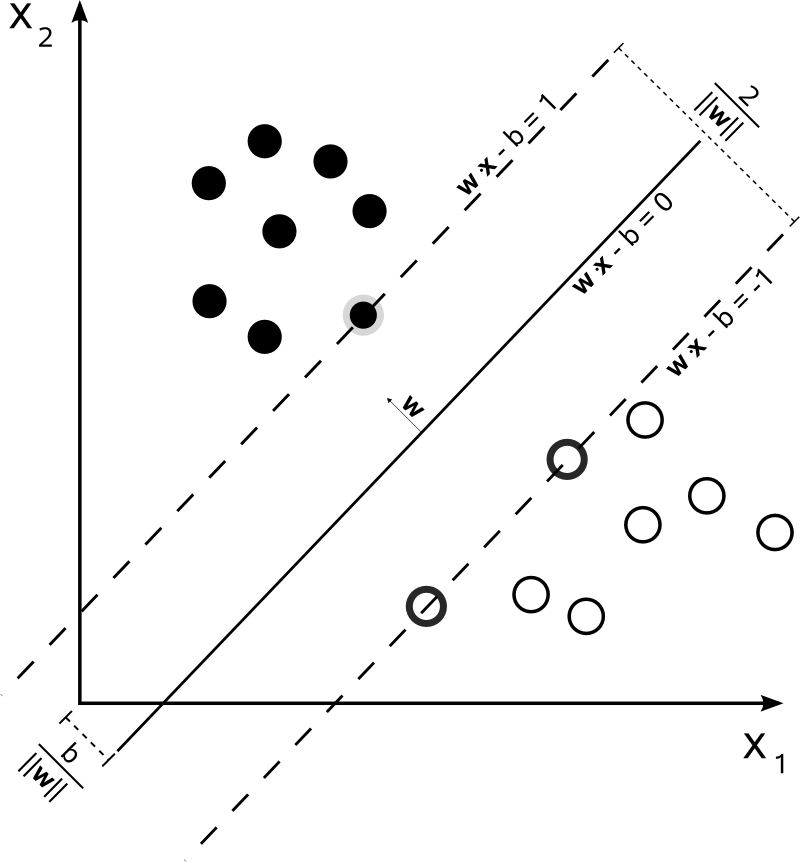
위 그림에서 검정원과 흰 원은 d(x) = wx+b 에 의해 두 부류로 나뉘어졌다. 이때, 그 선에서 가장 가까운 점을 support vector라고 한다.

L

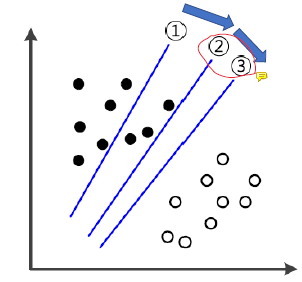
왜 여백을 최대화 해야하는가? 그 이유는 최대한 일반화 능력을 기르기 위함이다. 일반적인 모델은 1번에서 시작해서 점점 학습을 해나가다가 2번 선을 찾으면 학습을 종료할 것이다. 왜냐하면, train 데이터에 대해 100% 분류하는 선을 찾았기 때문이다. 하지만, SVM은 단순히 분류하는 것이 목표가 아닌 두 데이터 사이의 여백(간격)이 제일 큰 선을 찾는 것이 목적이기에 3번까지 도달해서야 학습이 끝난다. 
 

Linear SVM (선형 서포트 백터 머신)

 

1. Hard Margin

d(x) = w1x1 + w2x2 + ... + wdxd + b = WTx + b 식에서 우리는 여백을 가장 크게 하는 W와 b의 값을 구하는 것이 목표이다. 

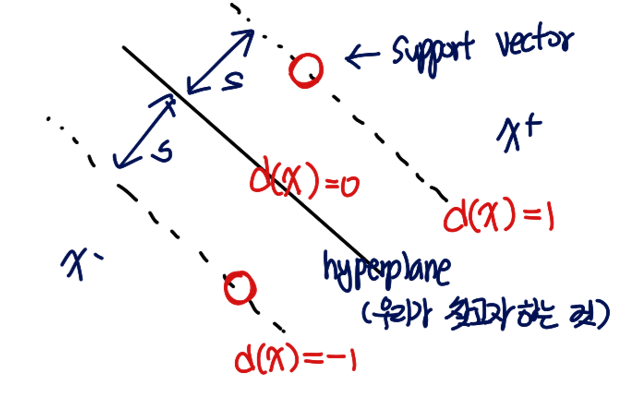
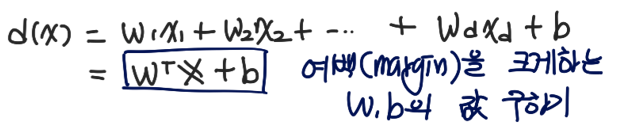
위의 진한 선이 d(x) = 0 선이다. 이 보다 위쪽에 있는 점들을 x+ 아래쪽에 있는 점들을 x-라고 하자. x+ 쪽의 support vector는 d(x) = 1 위에 있다. 그리고 x- 방향의 support vector는 d(x) = -1 위에 있다. 
즉, d(x+) = 1, d(x-) = -1이다. ( 이때, x+ = λw + x- 의 관계에 있다고 하자. )
아래 과정을 통해 λ를 구할 수 있다. 

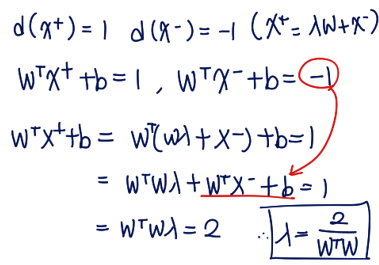
λ = 2 / W^T W 가 나온다. 이를 이용해 여백을 수식적으로 표현해보자.
margin = 2s = x+에서 x- 까지의 거리이다. 

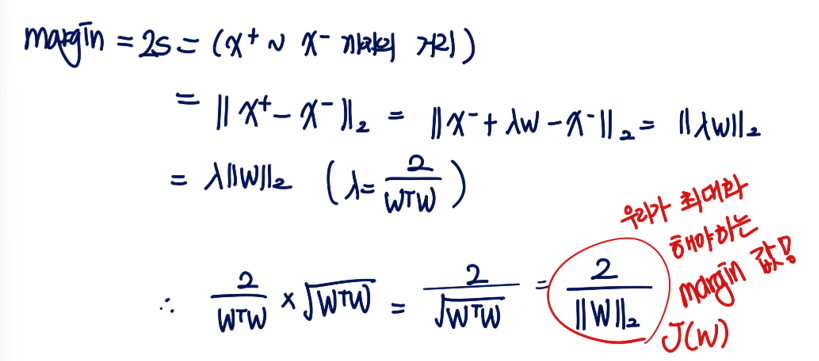
J(w) = 2 / ||w||_2 가 된다. 여기서 주의할 점은 ||n||_k 는 절댓값이 아니라, norm을 나타낸다. 
Norm은 vector의 사이즈이다. 

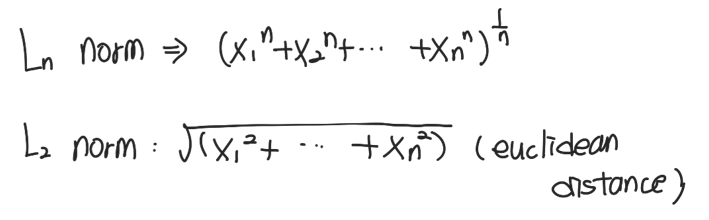
L2 norm이라는 것은 유클리드 distance랑 같은 의미라고 생각하면 된다. (norm에 대해서는 여러 규제 기법에 대해 정리할 때 한번 더 다루겠다. 원래 순서상 규제를 먼저 올려야했는데 )
 
SVM의 최종 목표는 Margin을 최대화하는 것이다. 

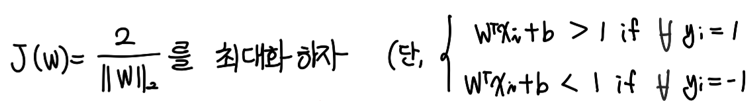
하지만, W가 분모에 있으니 문제가 복잡해져서 최대화 문제를 역수를 취하고 W에 제곱을 취해 최소화 문제로 고쳐보겠다. ( 제곱을 하는 이유는 l2 norm에 root 가 있어서 복잡해지기 때문 )

 
여기서 부터 조금 복잡해진다. J(W) = (||W||_2)^2을 어떻게 최소화 할까? 우리는 여기에 라그랑주 승수법을 적용할 것이다. 

https://terms.naver.com/entry.naver?docId=5938017&cid=60217&categoryId=60217

라그랑주 함수

이 지식백과에서 라그랑주 최적화 방법을 매우 쉽게 설명하고 있다. 참고하면 좋을 것이다. 
 
라그랑주 최적화에서의 목적함수는 J(w) 가 되고, yi(xiW^T+b) -1 가 제약 조건이 될 것이다. ( 단, 1<= i <= n )
목적함수와 제약조건을 하나의 식으로 만든 L(w, b, α) 는 아래와 같다.

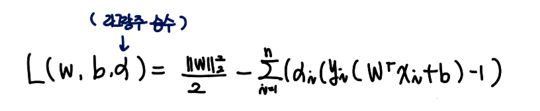
  여기서 α는 라그랑주 상수이다. 그리고 우리가 최종적으로 구하고 싶은 것은 W와 b 값임도 잊지 말자. 각각의 변수에 대해 편미분을 한 값이 = 0 임을 이용해 w, b의 값을 찾아보자.

정리한 식이 위(1, 2번 빨간 네모 식) 처럼 나왔다. 우리는 b, w를 구하기 위해서 최종적으로 라그랑주 상수에 해당하는 값인  α를 찾아야한다는 것을 알 수 있다. 
이렇게 구해진 1, 2번 식을 이용해 처음 L(w, b,  α) 식을 간단히 해보자. 

전개하면서, W와 b가 사라지고 α에 관한 식으로 변했다. 결국 Lagrangial Dual 문제로 변환이 된 것이다. 

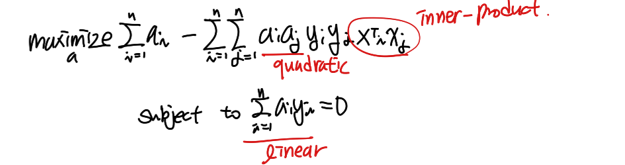
우리는 위  α에 관한 위 식을 최대화하는  α를 찾아야한다. 이때, 목적함수는  α에 대한 2차식이고 조건이 1차이기 때문에 KKT condition을 이용해  α 값을 구한다. 
https://en.wikipedia.org/wiki/Karush%E2%80%93Kuhn%E2%80%93Tucker_conditions

Karush–Kuhn–Tucker conditions - Wikipedia

KKT 에 대한 내용이다. 사실 나는 이해하지 않았다. 그냥 그렇구나 하고 넘어가는 게으른 학부생이다. 
KKT condition 은 Stationarity, Primal Feasibility, Dual Feasibility, Complementary slackness가 있다. 
Stationarity 가 우리가 아까 사용한 편미분 값이 0이라는 내용이다. 

여기서 우리는 complementary slackness에 집중해보자. 우리 식 L도 이 조건을 만족해야한다.

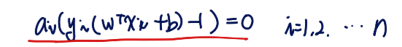
위 식을 만족해야한다. 이때, 두 가지 상황에 대해 살펴볼 수 있다. 첫 번째는 ai가 0인 경우이다. 이때는 yi(wTxi+b)-1 이 0이 아닐 수도 있다. ai 가 0보다 큰 경우는 yi(wTxi+b)-1 가 0이어야한다. 

즉, ai > 0 이면 support vector라는 의미이다. 

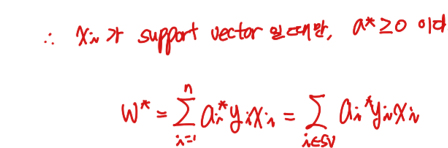
이렇게 W를 찾으면, b도 찾을 수 있다.
 
 

2. Soft Margin

위에서 찾은 식은 한 가지 한계가 있다. 바로, 점이 분리가능할 때만 사용할 수 있다는 것이다. 위와 같은 방식을 Hard Margin이라고 한다. 

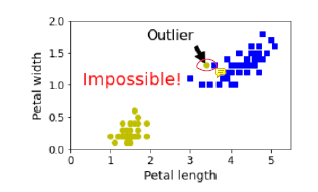
데이터에 outlier가 들어가있는 경우 등을 허용한다던지 등 약간의 규제를 풀어서 유연하게 SVM을 만들고자 한다. 그 방식을 Soft Margin이라고 한다. 

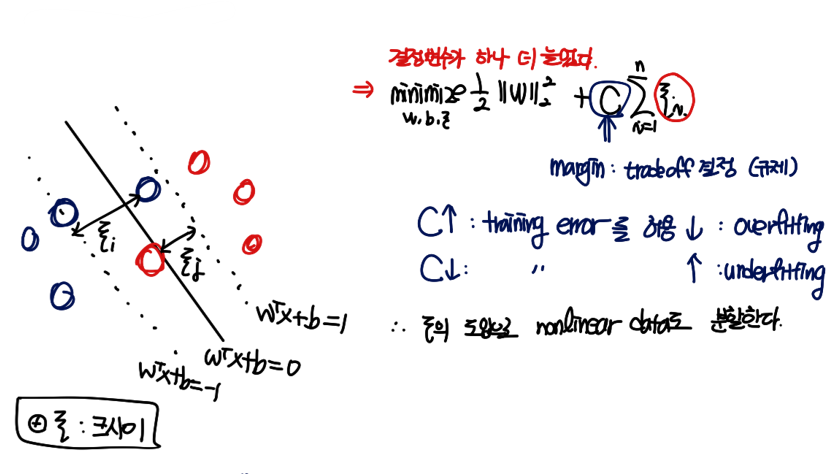
우리는 ξ 를 새로 정의 할 것이다. ξ는 정확하게 분류되지 않은 vector들이 초평면으로 부터 떨어진 거리이다. 그리고 이 것들의 합에 C를 곱한 값을 기존의 식에 더해 minimize 할 것이다. 이때, C는 사용자에게 받는 Hyperparameter이다. ( 코드 짤 때 넣는 그 변수 C 맞다. ) 
C를 크게 하면 상대적으로 정교해지기 때문에 overfitting 이 일어날 확률이 있고, C를 낮게 하면 margin의 범위가 넓어져 underfitting이 일어날 가능성이 있다. 이 값은 실험적으로 찾아야한다. 

라그랑주 식은 ξ 를 포함해 다음과 같이 변환된다. 
사실 이제 부터 앞에서 했던 과정과 동일하게 풀어나가면 되기에 설명은 생략하고 풀이과정만 보이겠다.

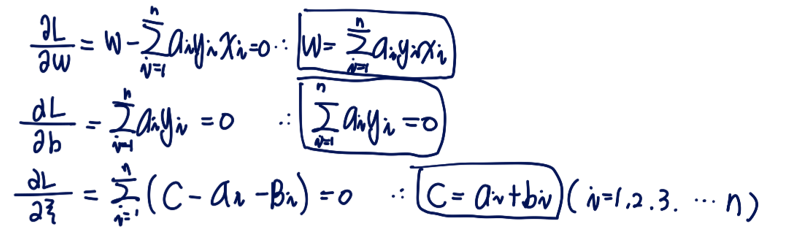
정말 놀랍게도 최종 식은 ai의 범위만 변한 결과가 나온다. 
 

왼쪽이 soft margin, 오른쪽이 hard margin이다.&amp;nbsp;

 

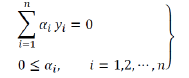
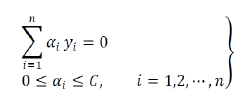
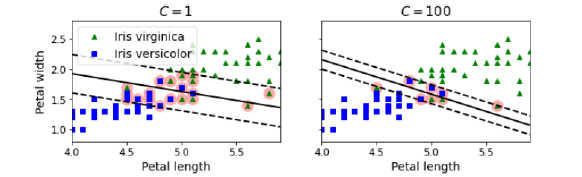
이렇게 C 값을 이용해 margin의 범위를 조정할 수 있다. 
 

Nonlinear SVM Classification

이때까지는 linear하게 데이터를 분리하고자 했다. 하지만, linearly seperable 하지 못하는 값이 약간의 공간 변형을 통해 linearly seperable한 상황이 온다면 공간 변형을 해서 나누면 될 것이다. 

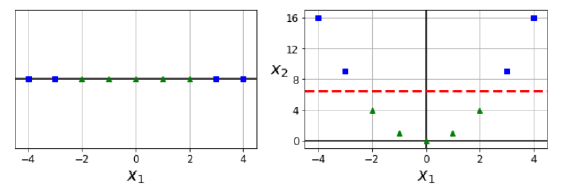
x2 = x1 ^ 2 이라고 하자. 위 사진에서 x1은 linearly seperable하지 않지만, 오른쪽의 경우는 쉽게 나눌 수 있다. 

여기서부터는 글이 길어져서 다음 글에서 이어지겠다.