[Algorithm] Strongly Connected Components (강한 연결 요소)
Connected Components
적어도 한 개 이상의 경로로 연결된 정점들로 구성된 종속 그래프이다. connected components는 단순히 연결되었는지 아닌지만 판단하면 되기 때문에 BFS나 DFS로 찾을 수 있다. ( Search가 가능하면 연결된거니까)
2023.06.13 - [Computer Science/Data structure & Algorithm] - [Algorithm] BFS, DFS
[Algorithm] BFS, DFS
그래프를 탐색하는 대표적인 방식에는 BFS와 DFS가 있다. 그래프 관련 알고리즘, 동적 프로그래밍 등 다양한 알고리즘 과정에서 응용된 형태로 많이 사용하기 때문에 알고리즘 공부를 할 때에는
mobuk.tistory.com
Strongly Connected Components (SCC)
강한 연결 요소는 connected component인 동시에 모든 정점이 다른 정점에 대하여 방문할 수 있는 경우를 의미한다. 비방향 그래프는 연결만 되어 있으면 항상 모든 정점이 다른 정점에 대해 방문할 수 있기 때문에 이 용어 자체는 방향 그래프에서만 사용한다.
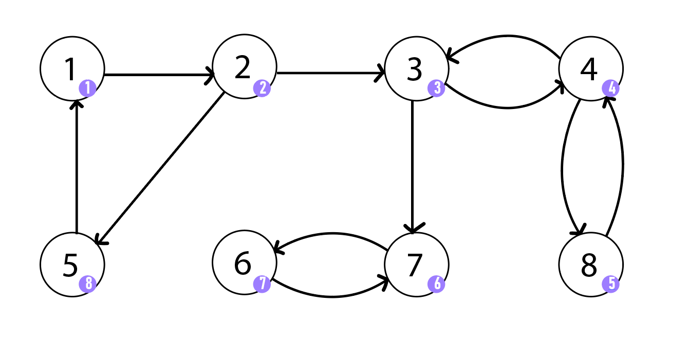
위 그림에서 1, 2, 5를 보자. 이들은 연결되어 있는 동시에 1은 2, 5를 방문할 수 있고, 2는 5, 1을 방문할 수 있고 5는 1, 2를 방문할 수 있다. 즉, 모든 정점이 다른 정점에 대해 방문할 수 있어서 {1, 2, 5} 는 strongly connected components이다.
하지만, 여기에 3이 추가된다고 생각해보자. 연결은 되어 있는데 3은 1, 2, 5를 방문할 수 없다. 즉, {1, 2, 3, 5} 는 strongly connected components가 아니다.
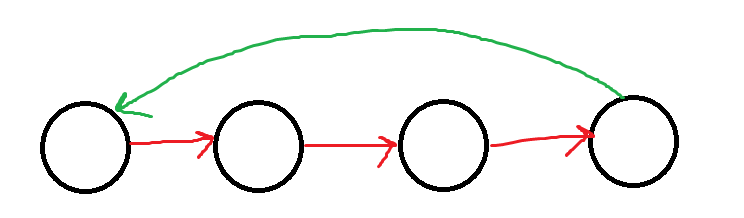
그럼 strongly connected components임을 어떻게 알 수 있을까? 한 노드에서 출발해서 다른 노드들을 거쳐 다시 자신 노드로 돌아오는 cycle이 형성되어 있으면 (즉, 출발지점인 부모로 돌아갈 수 있으면) 강한 연결요소라고 할 수 있다.
SCC를 찾는 대표적인 알고리즘은 2가지가 있다.
- 코사라주 알고리즘
- 타잔 알고리즘
적용 측면에서 더 유리하다고 알려진 타잔 알고리즘을 다룰 것이다. ( 그냥 사실 수업 때 이거만 배움 )
타잔 알고리즘(Tarjan's Algorithm)
기본 아이디어는 모든 정점에 대해 DFS를 수행하여 cycle이 되는 것을 찾는 것이다.
과정
모든 노드를 방문할 때마다 고유한 id 값을 매긴다. 이 id 값이 현재 부모를 나타낸다.
- 정점 1(부모 1)을 기준으로 DFS를 수행한다. 이때 정점은 stack에 넣어둔다.
- 정점 1과 연결된 정점 2(부모 2)를 스택에 넣으면서 DFS를 수행한다.
- 이렇게 반복해서 stack에 넣어준다.
- 더 이상 방문할 새로운 노드가 없으면서 본인의 부모 노드로 갈 수 있을 때는 정점 탐색을 종료한다.
- 더 이상 방문할 새로운 노그가 없으면서 본인의 부모 노드로 갈 수 없을 때에는 stack에서 본인 노드를 찾을 때 까지 꺼내준다. 이것이 본인을 노드로 하는 SCC이다.
- 모든 정점을 방문할 때 까지 반복해준다.
사실 과정을 글로 적어두면 무슨 말인지 알기 어렵다. 아래 예제 풀이와 함께 보는 것이 좋다.
예제 풀이
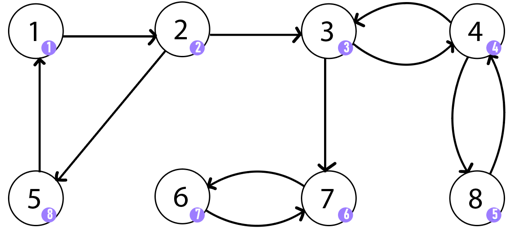
우리는 1번 노드부터 출발 할 것이다.
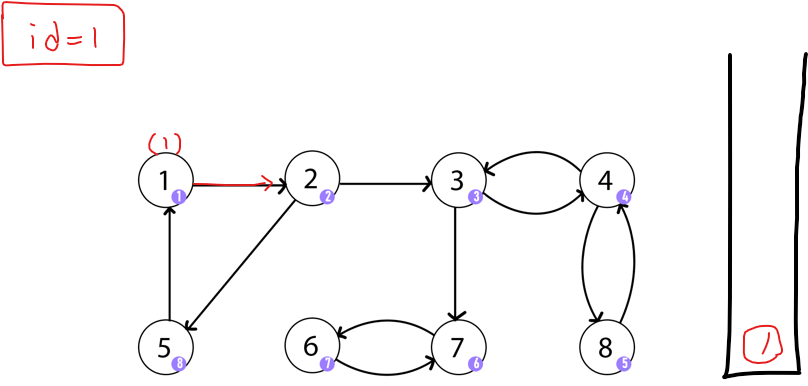
1번 노드에 id값을 기록하고 본인을 stack에 넣은뒤 연결된 2번 노드로 이동한다.
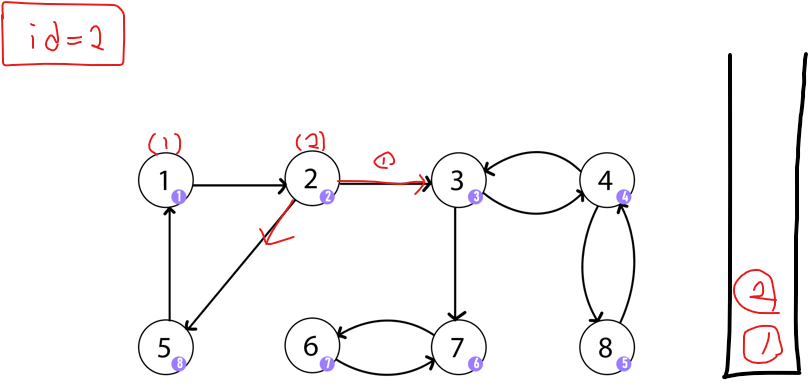
2번 노들르 방문하고 노드에 id 값을 기록한다. 그 뒤 두 가지 방향이 있는데 3부터 방문한다고 해보자. 이런 방식으로 8까지 방문한다.
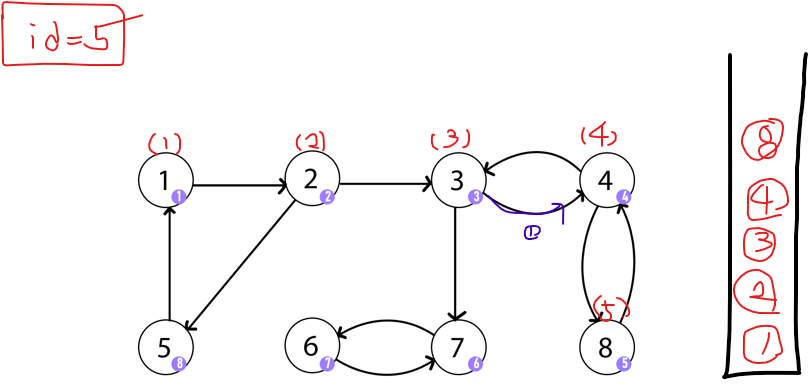
8까지 방문하니 더 이상 방문하지 않은 곳으로 이동할 수 없다. 이 때 8번이 연결된 노드들을 살펴보면 자신의 부모 노드로 이동할 수 있다. (본인의 id 값보다 작은 노드와 연결되어 있으면 => 8번은 4번 (id = 4)로 이동할 수 있다. ) 그러니 그냥 종료한다.(dfs(8)이 종료 -> 재귀가 한 겹 풀림)
dfs의 재귀가 풀리고 4에 도착한다. 4도 8과 같은 이유로 3, 8과 연결되어 있는데 3이 부모이기 때문에 재귀가 풀린다. 3은 아직 방문하지 않은 7이 있어서 방문한다.(id = 6이 됨) 그리고 6도 이어지니 방문하게 된다.
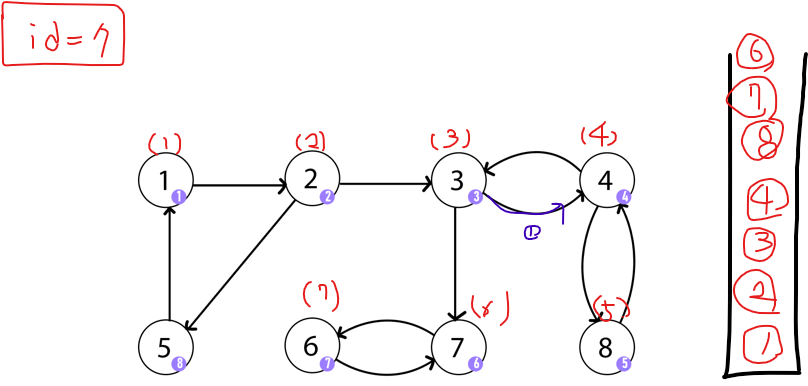
6에 도착한 순간 더 이상 방문하지 않은 정점으로 이동할 수 없으면서 이어진 정점이 부모로 추정되기 때문에 종료한다. (dfs(6) 종료 )

6에서 재귀가 풀리면서 7로 도착한다. 7의 경우는 앞의 경우와 다르다. 더 이상 방문하지 않은 노드로 이동할 수 없는 상태인 것은 동일하다. 하지만, 7에서 갈 수 있는 노드는 6밖에 없는데 6이 자신의 부모가 아니다. (6의 id 값이 7의 id 값보다 작다. ) 그래서 7은 SCC의 부모임을 알 수 있다.
그러니 stack에서 본인을 만날 때까지 요소들을 빼주면 된다.

이렇게 {6, 7} 쌍이 하나 만들어졌다.
이제 다시 3으로 돌아간다. 3은 더이상 방문할 곳이 없고, 7과 같은 상황으로 연결된 노드들 중 부모 노드로 갈 수 있는 경우가 없다. 그래서 stack에서 본인인 3을 만날 때 까지 꺼낸다. {3, 4, 8} 쌍이 만들어진다.

이제 3의 재귀도 풀리도 2로 간다. 2는 아직 5를 방문하지 않았기 때문에 5로 이동한다.
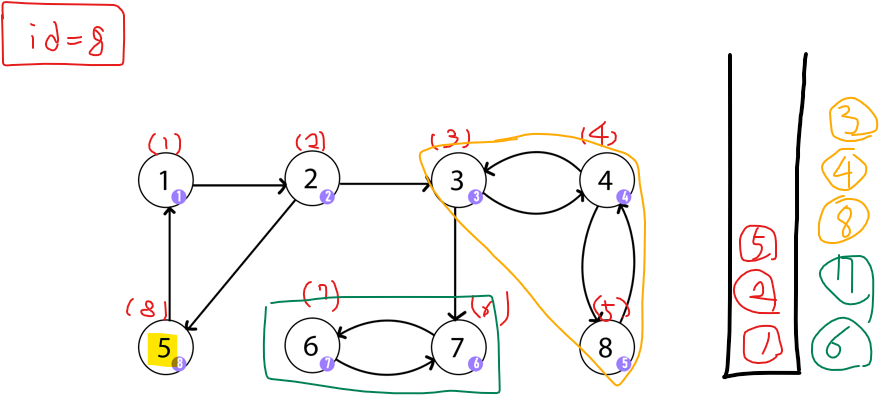
5는 방문하지 않은 노드 중 이동할 노드가 더 이상 없지만, 부모 노드로 갈 수 있어서 그냥 종료된다. 같은 원리로 2도 재귀가 풀린다.
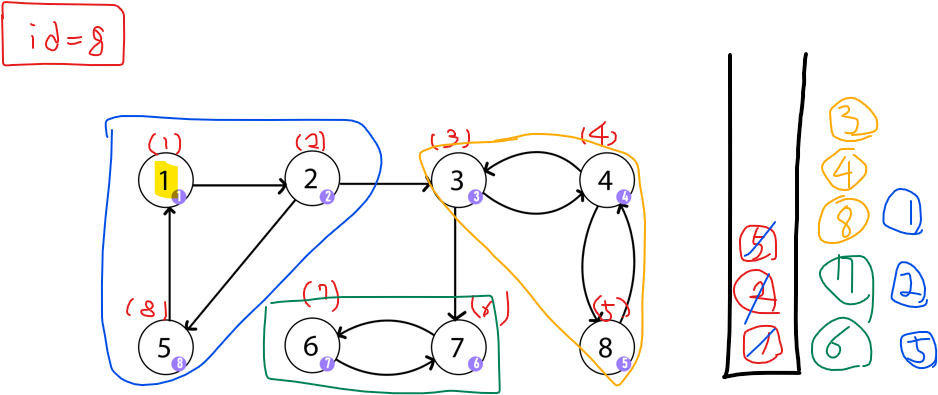
1로 도착하니 부모로 이동할 수 없으면서 방문할 곳도 없다. 그래서 stack에서 본인을 만날 때 까지 꺼낸다. 이렇게 {1, 2, 5} 가 얻어졌다.
이제 모든 정점을 방문했으니 dfs가 종료된다. 최종적으로 얻은 쌍은 {1,2,5}, {3,4,8}, {6,7}이다.
관련 문제
이 원리를 그래도 적용하면 되는 문제가 있다. 문제에 대한 정보와 풀이는 아래 글을 참고하자.
2023.06.13 - [Computer Science/Baekjoon] - [2150] python : Strongly Connected Component
'Computer Science > Data structure & Algorithm' 카테고리의 다른 글
| [Algorithm] Minimum Spanning Tree - Prim (0) | 2023.06.13 |
|---|---|
| [Algorithm] Minimum Spanning Tree - Kruskals (0) | 2023.06.13 |
| [Algorithm] BFS, DFS (0) | 2023.06.13 |
| [자료구조] Graph (0) | 2023.06.12 |
| [Algorithm] Dijkstra's Algorithm ( 다익스트라 알고리즘 ) (2) | 2023.06.10 |













