[Algorithm] Needleman-Wunsch algorithm
오늘은 Alignment algorithm 중 global alignment에 해당하는 Needleman-Wunsch algoritm(니들만 브니쉬) 에 대해 알아보겠다. alignment 알고리즘은 LCS (longest commen sequence) 알고리즘과 유사하다. LCS에 대해 궁금하면 아래 글을 참고하자.
[Algorithm] LCS (Longest Common Sequence)
DP의 대표 문제 중 하나인 LCS에 대해 다루어 보겠다. Longest Common Substring 공통 부분 문자열을 찾으라고 했을 때 우리는 보통 longest common substring을 생각하곤 한다. 이는 오늘 알아볼 LCS와는 다른 개
mobuk.tistory.com
1. Sequence Alignment
Sequence Alignment는 한국어로 '서열정렬'이라고 한다. 이에 대해 검색을 해보면 주로 '생물정보학'에서 DNA, RNA 사이의 기능적, 구조적 상관관계를 밝혀낼 때 주로 사용한다고 한다.

서열 정렬은 크게 두 가지로 분류할 수 있다.
- Global Alignment : 두 시퀀스의 전체 길이에 걸쳐 최적의 정렬을 찾는 문제로 전체 구조가 유사한 시퀀스들 사이에 적용하기 적합하다.
- Local Alignment : 두 시퀀스에서 가장 유사한 부분서열을 찾는 문제이다. 길이가 다르거나 일부 구조만 유사할 때 사용하기 적합한 방법이다.
오늘 알아볼 니들만 브니쉬 알고리즘은 Global Alignment에 해당하기 때문에 global alignment만 정리하겠다. Local alignment와 그에 해당하는 Smith-Waterman algorithm는 아래 글을 참고하자.
( 업데이트 되면 링크 달아두겠다. 1~2일 내로 업로드 예정)
우리는 서열정렬을 할 때, aligment score을 매겨 가장 점수가 높은 것을 취하는 것이 목적이다. 점수는 Match, Mismatch, Gap 세 가지로 나누어 줄 것이다.
- Match : 두 문자가 일치했을 때 => +1
- Mismatch : 두 문자가 다를 때 => -1
- Gap : 공백으로 처리할 때 => -2
예제를 한번 살펴보자.

공백의 위치를 어디에 두냐에 따라 X와 Y의 Alignment Score가 달라진다.
- case 1 ) X의 맨 마지막에 공백을 두었을 때

파란색이 Match, 빨간색이 Mismatch, 초록색이 Gap이다. 계산해보면 1 * 5 + -1 * 6 + -2 = -3이다.
- case 2 ) X의 _와 W 사이에 공백을 넣었을 때

10 * 1(Match) + -1 * 1 ( Mismatch) + -2 = 7
case 2의 경우가 case1의 경우보다 직관적으로도, alignment score 면에서도 좋은 모습을 보여준다. 우리는 이번 알고리즘을 통해 이 과정을 자동화 할 것이다.
2. Needleman-Wunsch algorithm
Score Matrix를 만들어 Match, Mismatch, Gap이 있는 상황 중 가장 값이 높은 것으로 채워갈 것이다. Score Matrix는 c로 표기하겠다.

여기서 S는 Match 일 때 1, Mismatch일 때 -1이다.
P는 -1이다.
S와 P의 값은 적절하게 설정해도 되는 것 같다. ( 내가 참고하여 공부한 영상에서는 Mismatch를 0으로 두었다.)

이렇게 이전 값을 채워나간다. 그리고 값을 채워나가면서 어디 방향으로 이동했는지도 기록해둔다. (대각선, 위, 왼쪽) 그럼 그 방향 정보를 바탕으로 backtracking하여 alignment한 결과를 알 수 있다.
3. 예제 설명
X = GCATGCG
Y = GATTACA
1. score table 생성 및 초기화
| Y(j) | G | C | A | T | G | C | G | |
| X(i) | 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 |
| G | -1 | 1 | 0 | -1 | ||||
| A | -2 | |||||||
| T | -3 | |||||||
| T | -4 | |||||||
| A | -5 | |||||||
| C | -6 | |||||||
| A | -7 |
위와 같이 table을 초기화 해준다.
2. 차례대로 table을 채워나간다. 값과 이동 방향을 모두 저장해두어야한다.
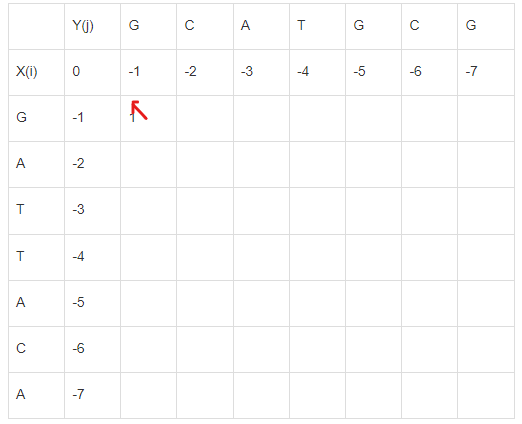
- c[1][1] : G와 G가 만난 상태이다. (match라 S가 1이 된다. P는 항상 -1)
max ( c[0][0] + S, c[0][1] + P, c[1][0] + P ) = max (1, -2, -2 ) = 1
- c[1][2] : G - C => mismatch로 S=-1
max( c[0][1] + S, c[0][2] + P, c[1][1] + P = max( -2, -3, 0 ) = 0

- c[1][3] : G-A => mismatch S = -1
max( c[0][2] + S, c[0][3] + P, c[1][2] + P) = max ( -3, -4, -1 ) = -1

같은 방법으로 표를 채운 결과이다.

가장 마지막 칸에서 backtracking 방식으로 화살표를 거슬러 올라가면서 실제 값을 확인한다.

파란색은 X의 공백, 초록색은 Y의 공백으로 생각하면 된다.
<결과> (편의상 공백은 _ 로 표현하겠다.)
X = G_ATTACA
Y = GCATG_CG
alignment score = 0
4. 관련 문제
아직 문제를 안찾아서 관련 문제를 해결하면 업데이트 하겠다.
'Computer Science > Data structure & Algorithm' 카테고리의 다른 글
| [algorithm] Floyd-Warchall algorithm (0) | 2023.05.24 |
|---|---|
| [algorithm] Smith-waterman algorithm (0) | 2023.05.22 |
| [Algorithm] LCS (Longest Common Sequence) (0) | 2023.05.21 |
| [Algorithm] Optimal binary Search (최적 이진 탐색 트리) (1) | 2023.05.20 |
| [자료구조] C - 스택(Stack) - 배열을 이용한 구현 (0) | 2022.02.12 |













