[AI] 강화 학습과 게임 지능 ( 강화학습, Salsa, Q 러닝, DQN )
강화 학습
보상 또는 페널티와 같은 피드백으로 에이전트의 학습 과정을 돕는 방법
- 강화학습과 지도학습의 비교
| 지도 학습 (신경망) | 강화 학습 | |
| 문제(데이터) | 훈련 집합 X와 Y | 환경 또는 환경에서 수집한 데이터 |
| 최적화 목표 | o 과 y의 오차인 |o-y| 최소화 | 누적 보상 최대화 |
| 학습 알고리즘이 알아내야 하는 것 | 오차 최소화하는 신경망의 가중치 | 누적 보상을 최대화하는 최적 정책 |
| 품질을 평가하는 함수 | 손실함수 | 가치함수 |
| 학습 알고리즘 | SGD | 동적 프로그래밍, Salsa, Q러닝, DQN 등 |
탐사형 정책과 탐험형 정책
에이전트가 주어진 state에서 어떤 action을 선택할지 결정하는 규칙이나 전략
- 탐사형 정책 (exploitation policy)
이미 알려진 영역이나 분야를 더 자세히 조사하고 연구하는 과정 - 탐험형 정책 (exploration policy)
미지의 영역이나 분야를 발견하고, 조사하며 이해하는 과정
탐험과 탐사 사이의 균형을 잘 맞추는 것이 중요하다. 너무 많은 탐험은 에이전트가 시간을 낭비하고 너무 많은 탐사는 에이전트가 최적의 해를 놓칠 수 있음.
=> 탐험과 탐사의 균형을 어떻게 맞출 것인가?
- 랜덤 정책 : 모든 경우를 랜덤으로 하는 것으로 가장 극단적으로 탐험하는 정책이다.
- E-탐욕 알고리즘 : 탐험은 E 비율만큼 진행하고, 나머지는 과거와 미래를 전혀 고려하지 않고 현재 최고 유리한 선택을 하는 탐욕 알고리즘을 실행하는 것.
강화학습을 위한 gym 라이브러리
openAI 재단이 만들어 배포하는 라이브러리로 여러가지 강화 학습 문제를 제공한다.
- FrozenLake
- CartPole
- MountainCar
- FetchSlide
- 아타리 게임
FrozenLake
S에서 시작하여 G로 도착하면 이기는 게임으로 F는 지나갈 수 있고 H는 구멍이라 빠지면 진다.

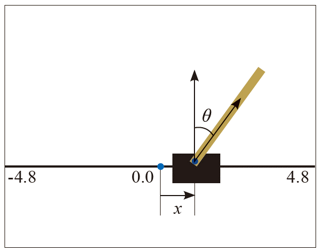
CartPole
수레를 좌우로 이동하여 수직 막대를 오래 유지하는 게임

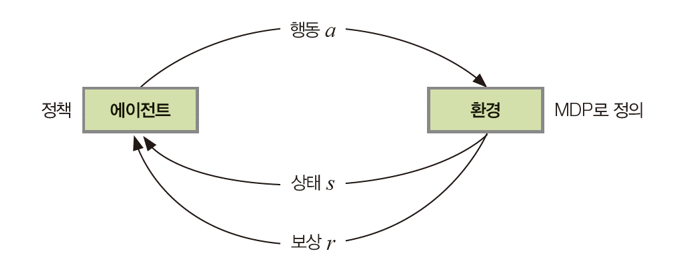
강화 학습과 최적 정책
계산 모형
마로코프 결정 프로세스 ( MDP : Markov decision process )

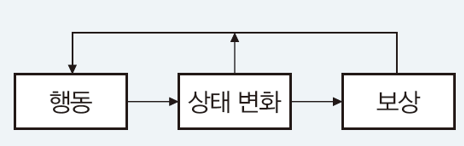
상태 전이
1. 결정론적 환경
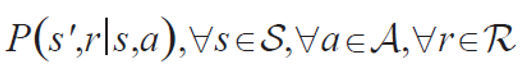
- s' : 새로운 상태
- r : 보상
- s : 현재 상태
- a : 행동
P(s' = 2, r = 0 | s = 1, a = 2) = 1.0
=> 상태 1에서 행동 2를 취하면 새로운 상태 2로 전환하고 보상이 0일 확률이 1.0이다.
위 예제는 새로운 상태가 정해지는 확률이 100%이다.
2. 스토캐스틱 환경
확률 분포에 따라 새로운 상태가 다르게 정해지는 환경
ex ) FrozenLake 문제에서 is_slippery 를 True로 설정했을 때
최적 정책
학습 알고리즘은 '누적(최종) 보상'을 최대화하는 '최적정책 (optimal policy)'를 알아내야한다. 최적 정책이란 모든 정책 중 가장 좋은 정책을 의미하며, 파이 위쪽에 ^ 기호를 붙여 표기한다.
정책은 확률 분포로 표현된다. P(a=i|s=j) 는 상태 s가 j일 때 행동 변수 a가 i라는 값을 취할 확률이다.

가치 함수
최적 정책을 찾기 위해 가치함수를 사용할 것이다. 가치함수란 상태 s에서 정책 파이를 따를 때 기대되는 누적 보상을 나타내는 함수이다.

이 중 최적 정책은 V_파이(s)를 최대화 해주는 정책이다.

가치 함수의 계산

위 식은 문제가 매우 커져 상태가 무한대로 변하면 적용하기 어려워 진다. 그래서 우리는 이전 상태를 이용할 것이다.

벨만 기대 방정식은 오른쪽 변에 자기 자신을 포함한 순환식 형태로 이루어져있다. 위 식은 salsa, Q러닝에 적용된다. 위의 식은 단순히 상태에 대해서만 나타낸 것이고, s와 a에 대해서도 나타낼 수 있다. (아래 식)

동적 프로그래밍
동적프로그래밍은 문제를 가장 작은 단위까지 분해한 다음 가장 작은 문제 부터 해결하기 시작하여 점점 큰 문제로 진행되는 상향식 문제해결 방법론이다. 정책 반복 알고리즘과 가치 반복 알고리즘이 있다.
정책 반복 알고리즘
입력 : 상태 전이 확률 분포
출력 : 최적 정책과 최적 가치 함수

3행의 가치함수 계산이 너무 많은 시간이 소요되어 잘 사용하지 않는다.
가치 반복 알고리즘
정책 반복 알고리즘에서 가치 함수 계산이 너무 오래 걸리는 것을 해결하기 위해 벨만 최적 방정식을 적용한 가치 반복 알고리즘이 등장하였다.

입력 : 상태 전이 확률 분포
출력 : 최적가치 함수

동적 프로그래밍은 부트스트랩 ( 이웃 상태와 정보를 주고 받으며 수렴해가는 방식 ) 이다. 하지만 마르코프 결정 프로세스를 알아야지만 적용가능하고 크기가 작은 문제에만 적용이 가능하다는 단점이 있다. ( 차원의 저주 )
학습 기반 알고리즘
동적 프로그래밍은 상태 전이 확률을 완벽하게 알아야만 적용이 가능하다. 상태 전이 확률이 없는 경우 환경을 시뮬레이션 하여 에피소드를 수집하여 학습시킬 수 있다.
에피소드와 훈련데이터 수집
에피소드 : 게임을 시작하여 마칠 때 까지의 기록

상태를 중심으로 에피소드를 잘라 데이터 수집을 한다. ( = 어느 순간의 상태부터 끝까지 잘라 데이터를 추출한다. )

몬테 카를로 방법
현실 세계의 현상 또는 수학적 현상을 난수를 생성하여 확률적 시뮬레이션 하는 기법
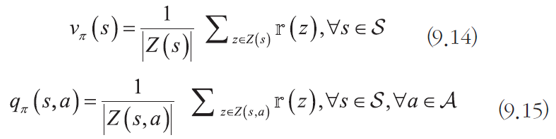
에피소드에서 얻어진 훈련 데이터를 수집하고 위의 식을 이용해 가치 함수를 계산한다. 에피소드 생성할 때 주로 난수를 사용하기 때문에 몬테카를로 방식이라고 한다.
몬테 카를로 방법은 데이터를 활용하기 때문에 학습기반이지만, 이웃 상태의 정보를 고려하지 않는다. ( 부트스트랩 방식이 아니다. )
시간차 학습 알고리즘 (Time-Difference learning)
동적 프로그래밍의 부트스트랩 방식과 몬테카를로 방식의 학습기반 장점을 결합한 방식이다. 가치 함수를 개선할 때 종료까지 가는 것이 아닌 이웃 상태만 본다.

시간차 학습 알고리즘 공식 유도 과정
1. 에피소드 e에서 t 순간에 추출한 샘플 z에 대해 처리한다고 생각하자.

2. z에 대해 가치함수 식을 다시 쓴다.
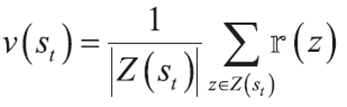
3. z가 k번째에 추가된다면 식을 다시 적을 수 있다.
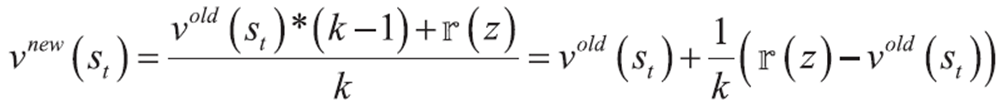
이미 구해진 평균에서 새로운 값을 넣을 때와 유사하게 작동한다고 생각하면 쉽게 이 식을 이해할 수 있다.
4. 첨자를 제거하고 1/k를 p로 치환한다.

위 식은 r(z) 때문에 누적 보상액을 알아야해서 부트스트랩 방식이 아니다. 그래서 r(z)를 이웃의 상태인 s', r로 표현해야한다.
5. r(z)를 r_t + γv_π (s_(t+1))로 대치한다.
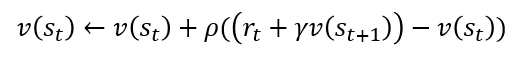
위 식은 에피소드를 사용하면서 동시에 부트스트랩 방식이다. 이 식을 적용하여 학습한 것이 대표적으로 sarsa와 Q러닝이 있다.
+) 위 식은 상태 가치 함수이다. 행동가치 함수로 나타내면 아래와 같다.

Sarsa
s - a - r - s' - a' 고리를 만들고 시간차 학습 알고리즘을 적용하여 가치함수를 개선하는 방식이다.

on-policy (켜진 정책) 방식이다. ( 행동 a'을 결정할 방법이 없어 현재 가치함수에만 의존한다. ) 정책에 따라 행동을 취하고 q-function을 업데이트 한다.
Q 러닝 ( Q - learning )
가치 함수 q에 의존하지 않고 max 연산자를 사용한다. 정책에 의존하지 않기 때문에 off-policy(꺼진 정책) 방식이다.


상태 가치 함수를 표현하는 v, 행동 가치 함수를 표현하는 q는 각각 1차원과 2차원 배열이다. 이 것을 사용하는 알고리즘을 참고표 방식이라고 한다. 하지만, 상태의 개수가 방대하면 참조표 방식이 비현실적이게 된다. 그래서 참조표 없이 가치 함수를 계산 하는 방식인 DQN이 등장하게 되었다.
DQN
딥러닝과 Q 러닝을 결합한 모델이다. 가치 함수 상태를 저장하고 계산하는 참조표 방식에서 벗어나 신경망을 적용해 가치 함수를 추정한다.

훈련 집합 수집 방법
Q 러닝에서 생성되는 에피소드로부터 샘플을 수집한다. 개선된 추정치를 레이블로 간주하고 훈련 샘플을 수집한다.
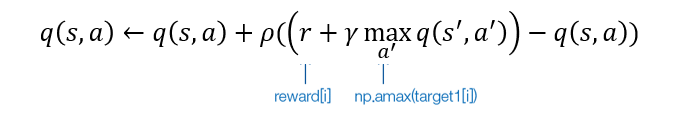
하지만, 이렇게 수집하다 보면 샘플 간의 상관관계가 너무 높아 overfitting이 발생할 수 있다. 그래서 '리플레이 메모리'를 이용해 학습한다.
- 리플레이 메모리 (experience replay memory)
훈련 샘플을 추출할 때 바로 신경망에 학습 시키는 것이 아닌 리플레이 메모리에 저장한다. 이후 미니배치를 구현하여 학습을 수행한다.
'Computer Science > AI' 카테고리의 다른 글
| [MIT 6.S191] Recurrent Neural Networks, Transformers, and Attention (0) | 2023.09.27 |
|---|---|
| [MIT 6.S191] Introduction to Deep Learning (0) | 2023.09.13 |
| [AI] DCNN Architecture (AlexNet, VGGNet, GoogLeNet, ResNet) (0) | 2023.06.11 |
| [AI] 생성 모델 ( 오토인코더, GAN, PixelCNN, PixelRNN ) (0) | 2023.06.11 |
| [AI] 시계열 데이터와 순환신경망 (RNN, LSTM) (0) | 2023.06.11 |













