[MIT 6.S191] Introduction to Deep Learning
All materials are copyrighted and licensed under MIT license.
© Alexander Amini and Ava Amini
MIT Introduction to Deep Learning
IntroToDeepLearning.com
MIT Deep Learning 6.S191
MIT's introductory course on deep learning methods and applications.
introtodeeplearning.com
MIT에서 2023년 3월 10일부터 5월 12일까지 매주 아침 10시에 진행된 Introduction to Deep learning 강좌가 진행되었다. 이 강의는 매년 진행되는 것으로 보이고, 학교 교수님께서 혼자 인공지능을 더 깊게 공부하고 싶은 사람 중 기초 강좌로 보기 좋다고 하셔서 이번 학기에 매주 영상을 보고 정리하는 시간을 가지려고 한다.
이 강의 자료에 대한 모든 저작권은 MIT 에 있으며, 관련 자료가 필요하신 분은 위 사이트로 들어가면 누구나 자료를 다운받을 수 있으니 참고하길 바란다.
https://www.youtube.com/watch?v=QDX-1M5Nj7s&list=PLtBw6njQRU-rwp5__7C0oIVt26ZgjG9NI&index=1
Contents
- Why Deep learning and Why now?
- Deep learning이 무엇인가?
- 왜 최근에 들어서 딥러닝의 중요성이 높아지는가? - Neural Network
- Perceptron
- Multi Output Perceptron
- Single Layer Neural Network
- Deep Neural Network - Activation Function
- Loss function
- Binary Cross Entropy Loss
- Mean Squared Error Loss - Loss Optimization
- Learning Rate
- Adaptive Learning Rate - Mini-batch
- Overfitting
- Dropout
- Early Stopping
Why Deep learning and Why now?
Deep learning이 무엇인가?
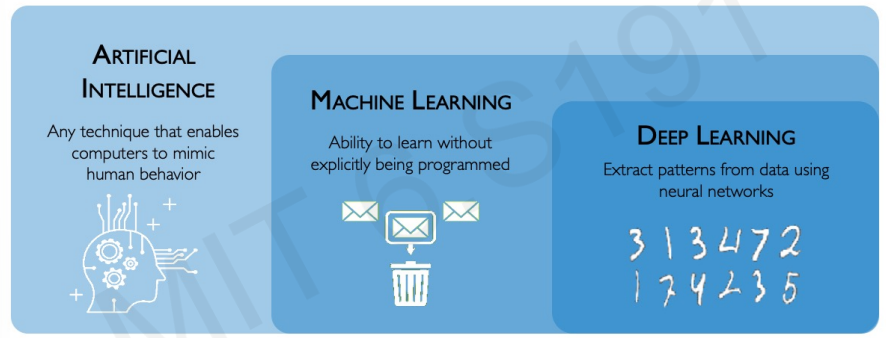
AI : 사람의 행동을 따라하는 능력을 가진 기술
ML : 미리 프로그램되지 않고 학습하는 능력
DL : 신경망을 사용하여 패턴을 추출하는 것
Deep learning 기술은 data에서 어떻게 특징을 추출할 것인가에 집중한다.
ex) 사람의 얼굴의 특징을 추출한다고 해보자.
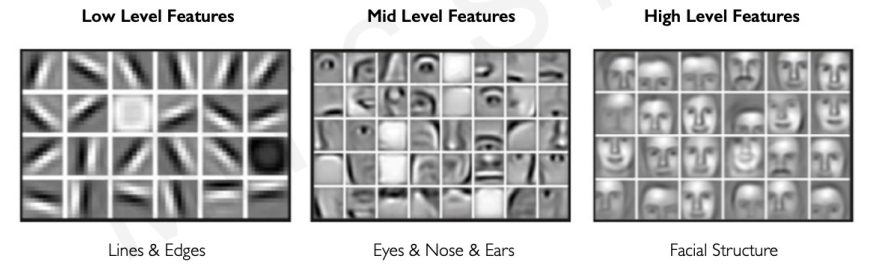
low level에서는 선과 모서리들로 이루어져 있을 것이고 조금 더 높은 단계의 특징은 눈,코,입 등이 있을 것이다. 매우 높은 차원의 특징은 얼굴 구조들이 있을 것이다.
이러한 특징을 추출하는 것을 수작업으로 진행하다보면 확장성도 없고 시간도 오래 걸린다. 그래서 머신러닝을 도입해 데이터로부터 직접 특징을 추출한다.
이러한 작업은 수십년 전부터 이루어지고 있었고 현대의 기술까지 이어졌다.
왜 최근에 들어서 Deep learning의 중요성이 높아지고 있는가?
딥러닝을 하기 위해서는 3가지 조건이 필요했다.
1) Big data
2) Hardware
3) Software
최근 기술의 발전으로 위 세가지의 요건이 충족되면서 딥러닝의 발전이 가속화 되기 시작했다.
Neural Network
Perceptron
퍼셉트론은 신경망의 가장 기본적인 구조로 여러개의 input을 처리해서 하나의 output을 도출한다.

기본 구조는 위와 같다. 여러개의 input에 각각의 weight를 곱하여 이를 더한 뒤 비선형성을 적용하여 결과를 도출한다. 위 구조를 식으로 나타내면 아래와 같다.

위의 식이 가장 직관적이긴 하나, 선형적으로 표현하면 차원이 높아질 수록 표현이 쉽기 때문에 우리는 아래와 같은 방식으로 표현할 것이다.

w0는 bias라고 한다. bias는 input이 1일 때의 weigth 값이다. g는 activation function(활성함수) 이다. 선형적으로 계산된 결과를 활성함수에 통과시켜 최종 결과 값을 얻어낸다. (활성함수에 대한 이야기는 뒤에 나온다)
이러한 과정들이 앞에서부터 순차적으로 이루어지기 때문에 forward propagation이라고 한다. (뒤쪽의 backpropogation이 나올 때 차이점을 잘 느껴보길..)
Multi Output Perceptron
지금까지 살펴본 퍼셉트론은 여러개의 input이 있으면 하나의 output을 내는 것이었다. 이제 output을 여러개로 확장시켜 볼 것이다.

각각의 output을 구분하기 위해 아래 첨자를 붙여 표현하겠다.
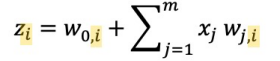
모든 input은 모든 output에 연결되어 있다. 그래서 우리는 이 layer를 Dense layer라고 부를 것이다. 이 것을 코드적으로 구현할 수 있다.
import tensorflow as tf
# 내부 구조를 직접 구현하는 방법
class MyDenseLayer(tf.keras.layers.Layer):
def __init__(self, input_dim, output_dim):
super(MyDenseLayer, self).__init__()
self.W = self.add_weight([input_dim, output_dim])
self.b = self.add_weight([1, output_dim])
def call(self, inputs):
z = tf.matmul(inputs, self.W) + self.b
output = tf.math.sigmoid(z)
return output
# tensorflow의 Dense를 사용하는 방법
layer = tf.keras.layers.Dense(units=2)
Single Layer Neural Network
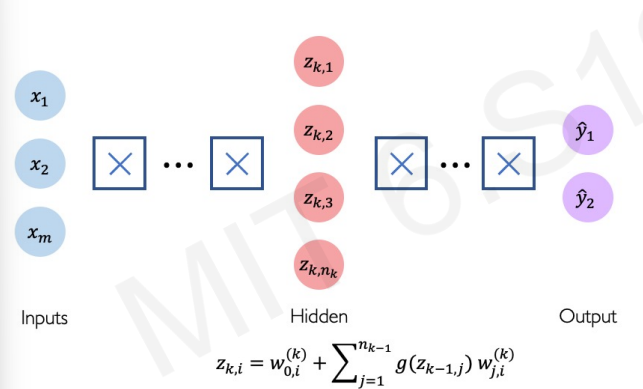
이제 조금 더 복잡한 신경망 형태를 볼 것이다. 안쪽에 layer를 하나 추가했다.

은닉층이 하나 추가되면서 조금 더 복잡한 문제를 해결할 수 있는 형태가 되었다. 구조도 약간 복잡하기 때문에 일부분을 먼저 살펴보겠다.

위처럼 살펴보면 사실 이때까지 살펴본 간단한 구조와 완벽히 같다. 하지만, 변한 것은 가중치가 어디를 의미하는지 나타내개 위해 붙은 여러 숫자들이 있다는 것이다.
W의 위쪽에 붙은 괄호 속 숫자는 어디 layer에 속해있는지 알려준다. W의 아래쪽의 숫자를 n,m이라 하면 n번째에서 출발해 m번째로 도착한다는 의미이다.

위 과정을 수식적으로 정리하면 다음과 같다. (기본 형태는 변하지 않았다)
그리고 앞으로는 Fully Connected 되어있는 모습을 일일히 선으로 나타내지 않고 아래와 같이 표현하기로 한다.

Deep Neural Network
깊은 신경망은 은닉층을 깊게 쌓으면 된다.
Activation Functions
한 가지 안짚고 넘어간 것이 있다. 바로 활성함수이다. 강의에서는 perceptron하면서 바로 다루는데 글로 정리하다 보니 따로 정리하는게 읽기 편할 것 같아 지금 다룬다.
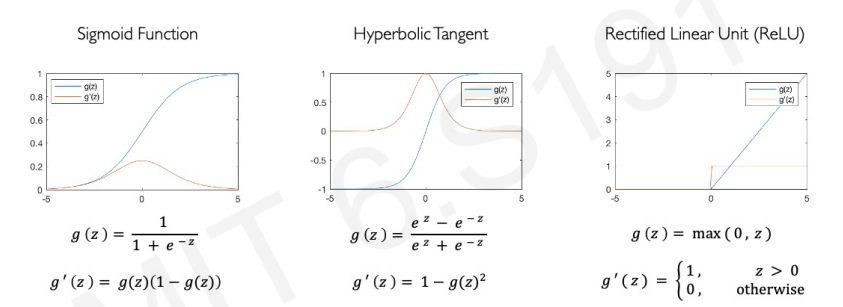
- sigmoid function
0과 1사이의 숫자로만 output을 출력한다. 결과 값이 확률분포일 경우 표현하는데 굉장히 유리하다. - hyperbolic tangetn
- Rectified Linear Unit (ReLU)
도함수를 구할 때 z = 0 부분을 제외하고는 굉장히 간단하게 값이 나온다.
이러한 활성함수들은 왜 비선형적일까?
데이터에 비선형성을 도입하면 데이터를 유연하게 분류할 수 있다.

왼쪽이 선형적인 경우, 오른쪽이 비선형적인 경우이다. 비선형성을 도입하면 확실히 데이터를 더 유연하게 분류할 수 있다는 것을 확인할 수 있다.
Loss function
신경망을 완성시켰으면 이제 실제 예에 적용할 차례이다.
간단한 문제를 통해 그 과정을 따라가보겠다.

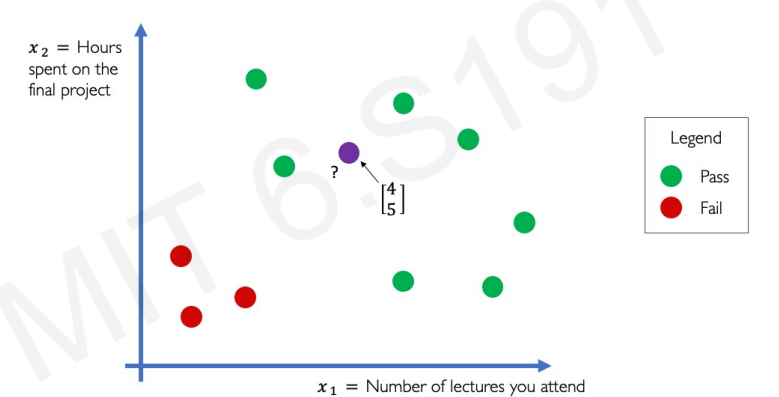
위의 그래프 상황에서 새로운 보라색 데이터가 들어왔다. 보라색 학생은 Pass일까? Fail일까? 직관적으로 pass가 나오는 것이 맞다고 생각이 든다.
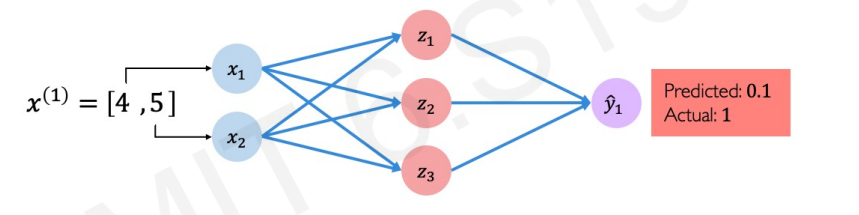
두 개의 특징벡터(input), 하나의 output이 있고 은닉층이 1층 있는 위와 같은 신경망을 만들고 우리의 새 데이터를 넣으니 pass할 확률을 구했더니 0.1 (10%) 가 나왔다.
왜 이런 일이 일어난 것일까?
=> 바로 아직 학습이 되지 않은 신경망에 값을 넣었기 때문이다.
처음 신경망을 구축하면 어떠한 학습도 되어 있지 않다. 우리는 이 신경망을 여러 데이터를 넣어 학습을 시켜야한다. 학습을 시키는데 필요한 요소가 Loss이다.
Loss는 실제 값과 예상 값의 차이를 의미한다.

신경망의 최종 목표는 Loss를 최소화 시키는 것이다. 이 loss를 구하는 방식을 함수로 만든 것이 loss function이다.
(참고로 loss function, cost function, empirical risk, objective function은 모두 같은 뜻으로 사용된다.)

대표적으로 2가지 loss function을 알아보자.
Binary Cross Entropy Loss

0과 1사이의 확률로 나타낸다.
(mit에서 개발했다고 한다)
Mean Squared Error Loss (MSE)

차이의 제곱의 평균이다. loss function 중 가장 간단한 형태라고 생각한다. binary cross entropy와는 다르게 실제 값의 오차로 계산된다.
Loss optimization
위에서도 언급했는데 결국 딥 러닝의 목표는 loss를 최소화하는 것이다. loss를 최소화 할 수 있는 weight를 찾아야한다.

loss를 최적화하는 알고리즘에 대해 알아보자.

1. 가중치를 랜덤하게 초기화한다.
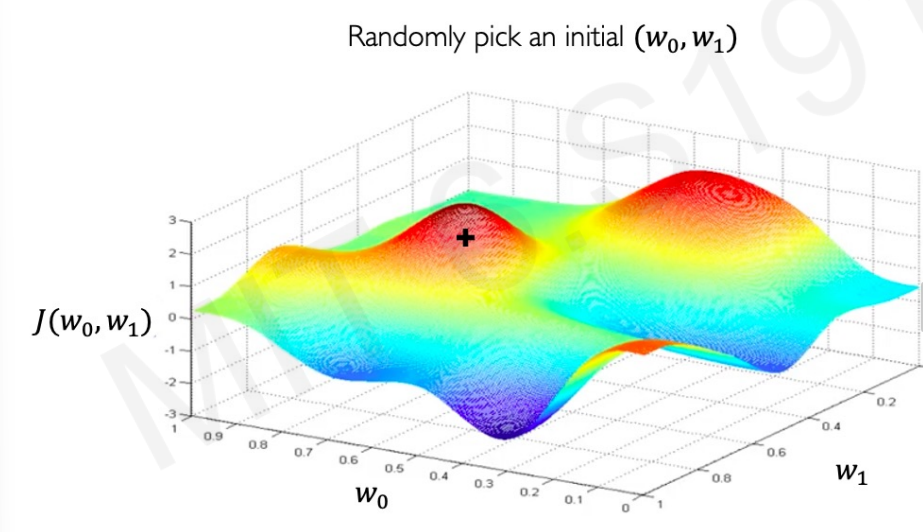
2. gradient를 계산한다.
이때, 편미분을 사용하는 이유는 고차원으로 넘어갈 수록 여러 변수에 대해 미분을 하는 것이 굉장히 어렵기 때문이다.
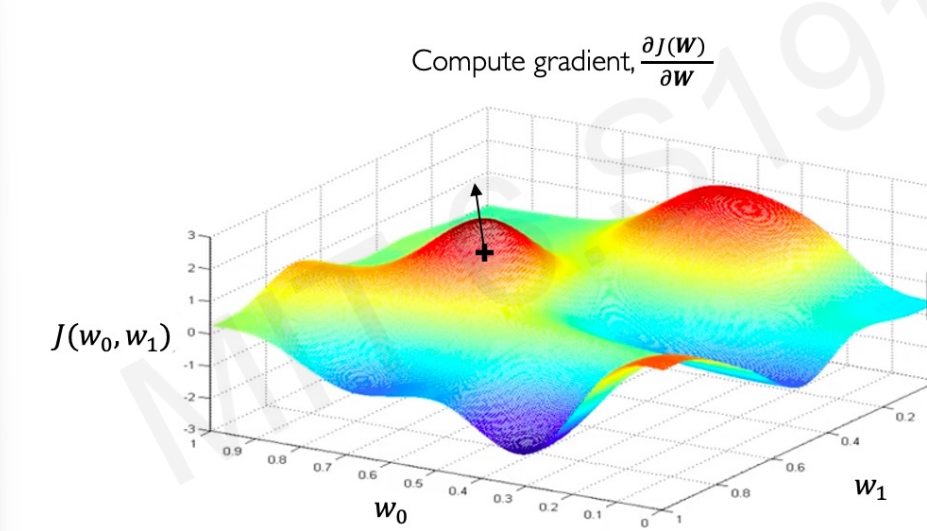
3. weights를 gradient의 반대 방향으로 업데이트한다.

왜 반대방향일까?
위 그림에서 예시를 들면 가장 낮은 구간을 찾아야한다. gradient가 증가한다는 것은 가중치가 커질수록 더 높은 구간으로 이동할 것이라는 의미이다. 우리는 가중치가 감소하는 곳으로 가야하기에 감소하는 곳 (즉, 반대쪽)으로 이동해야한다. 반대로, 감소하는 구간이면 가중치가 커질수록 감소한다는 것이다. 그러니 가중치가 증가하는 쪽으로 가야하기에 반대로 이동해야한다.
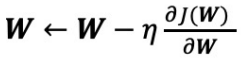
그래서 gradient에 - 를 붙여 업데이트 해준다. (n처럼 생긴 저 것은 학습률인데 뒤쪽에서 이야기 할 것이다)
import tensorflow as tf
weights = tf.Variable([tf.random.normal()])
while True:
with tf.GradientTape() as g:
loss = compute_loss(weights)
gradient = g.gradient(loss, weights)
weights = weights - lr * gradient
Backpropagation
우리는 gradient를 구하는 부분에 잠깐 집중을 해보겠다.


W2를 변경시켰을 때 J(W)가 어떻게 변하는지 알고 싶다.

우리는 이 값을 chain-rule를 통해서 구할 것이다.

위 식을 잘 살펴보면 뒤쪽에서 부터 앞으로 거슬러 올라온다. 그래서 우리는 이것을 backpropagation, 즉, 역전파라고 한다.
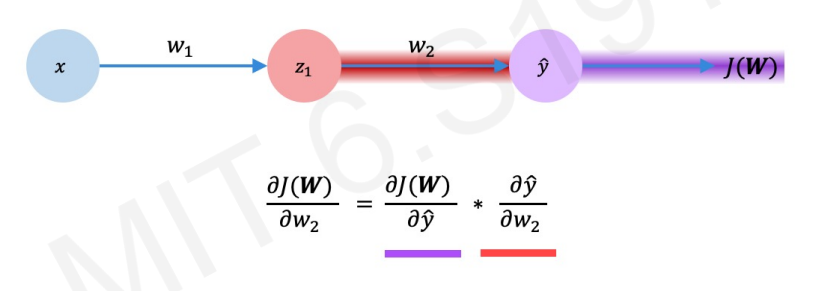
w1도 chain rule을 이용하여 같은 방식으로 구현할 수 있다.

Learning Rate

gradient를 수정할 때 learning rate를 곱해준다. 학습률이란, 얼마만큼 weight에 영향을 줄 것인지 정하는 것이다.
학습률이 너무 낮으면, 너무 천천히 수렴해서 결국 원하는 값에 도달하지 못할 것이다. 반대로 학습률이 너무 높으면, 수렴하기 못할 것이다. 그럼 최적의 학습률은 어떻게 찾을 수 있을까?
1. 그냥 해보면서 찾자.
2. adaptive learning rate를 사용하자.
adaptive learning rate
학습률은 더이상 고정되어 있지 않다. 얼마나 gradient가 큰지, 학습이 얼마나 빠른지 등 여러 요인을 고려해 변화한다. 이를 위한 알고리즘 들이 있다.
이미 여러개 구현 되어 있으니 여러개를 사용해보면서 최적인 학습률을 찾으면 된다.
Mini-batches

gradient를 구할 때 각각의 데이터에 대해 모두 계산했다. 작은 데이터셋에서는 괜찮지만, 데이터 셋이 많아지면 이는 너무 비용이 높아진다. 그래서 우리는 데이터를 묶어서 이 과정을 한꺼번에 진행하는 방법을 고안해냈다.
Stochastic Gradient Descent

gradient 계산을 묶어서 한다는 것 밖에 변하지 않았다.
Overfitting
한 가지 중요한 개념이 더 있다. 바로 overfitting (과잉적합)이다.
신경망이 너무 깊어지면 train dataset에 대해 과잉적합이 일어나서 일반화 능력이 떨어지게 된다.

이를 방지하기 위한 대표적인 2가지 방법이 있다.
Dropout
랜덤으로 layer의 연결을 끊는 것이다.

일반적으로 50%를 많이 선택하며, 이러면 계산도 빨라지고 신경망의 과잉적합을 막을 수 있다.
Early Stopping
오버피팅이 일어나기 전 학습을 중단시키는 것이다.
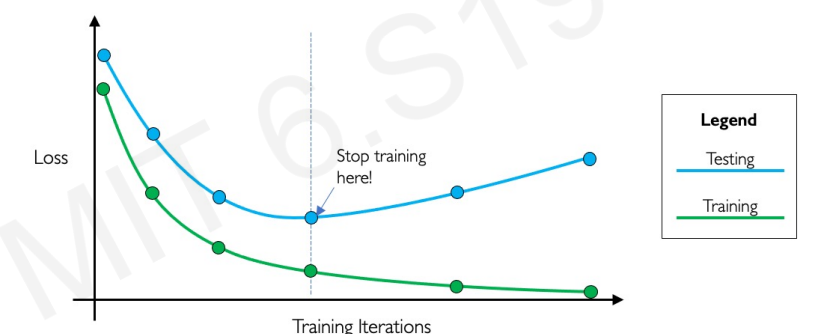
일반적으로 학습할 수록 test 셋에 대한 loss도 함께 줄어들어야한다. 하지만, train 셋의 loss는 감소하는데 test 셋의 loss가 증가하면 오버피팅이 일어난다는 의미이다. 그 지점이 발견되면 학습을 중단하는 것이다.
Review
'Computer Science > AI' 카테고리의 다른 글
| [AI] Ensemble Learning - Voting, Bagging, Boosting, Random Forests (2) | 2023.10.17 |
|---|---|
| [MIT 6.S191] Recurrent Neural Networks, Transformers, and Attention (0) | 2023.09.27 |
| [AI] DCNN Architecture (AlexNet, VGGNet, GoogLeNet, ResNet) (0) | 2023.06.11 |
| [AI] 생성 모델 ( 오토인코더, GAN, PixelCNN, PixelRNN ) (0) | 2023.06.11 |
| [AI] 강화 학습과 게임 지능 ( 강화학습, Salsa, Q 러닝, DQN ) (0) | 2023.06.11 |













