[AI] 컴퓨터 비전 - 영역 분할 (고전적인 기법을 중심으로)
https://m.hanbit.co.kr/store/books/book_view.html?p_code=B8870109394
IT CookBook, 컴퓨터 비전과 딥러닝
규칙 기반의 고전 컴퓨터 비전을 지원하는 OpenCV와 데이터 중심의 딥러닝 컴퓨터 비전을 지원하는 텐서플로를 활용한 85개 파이썬 프로그램으로 컴퓨터 비전을 균형 있게 배울 수 있습니다.
m.hanbit.co.kr
위 도서를 기반으로 정리한 내용이며, 일부 내용이 없거나 추가되었을 수 있습니다. 자세한 내용을 알고 싶으면 위 책을 참고하여 주세요.
4.1 에지 검출
영상의 미분
미분 : x가 매우 미세하게 증가했을 때의 함수의 변화량

디지털 세계에서는 최소 변화량이 1이다. 따라서 f'(x) = f(x + 1) - f(x)로 표현할 수 있다. 우리는 이 것을 필터 u에 적용하여 컨볼루션 형태로 미분을 한다.
| - 1 | 1 |
필터 u가 위 처럼 구성 되는 이유는 f(x)의 계수가 -1 ( 왼쪽칸 ) f(x+1)의 계수가 +1 이기 때문이다. f(x)의 x는 위치를 나타낸다고 생각하면 쉽다.
위 미분 방법을 사용하면, 계단형식으로 변화하는 에지를 검출할 수 있다.
| 2 | 2 | 2 | 7 | 7 | 7 | 7 |
| -1 | 1 |
원래 영상 f(위) 에 필터 u(아래)를 적용하면 결과는 아래와 같다.
| 0 | 0 | 5 | 0 | 0 | 0 | - |
결과는 2와 7의 경계인 부분의 값이 5로 잘 검출된 것을 알 수 있다. 경계가 뚜렷할 수록 해당 값의 절댓값은 커질 것이다.
에지 연산자
위의 미분을 이용한 방식은 명함이 계단 형식으로 변화할 때는 사용할 수 있다. 하지만, 현실세계의 화소는 여러 화소에 걸쳐 변화하는 램프 에지가 발생한다. 즉, 두께가 1보다 큰 에지가 발생한 것이다. 그럼... 물체 경계가 사실은 하나인데 여러개로 탐지될 수도 있다.
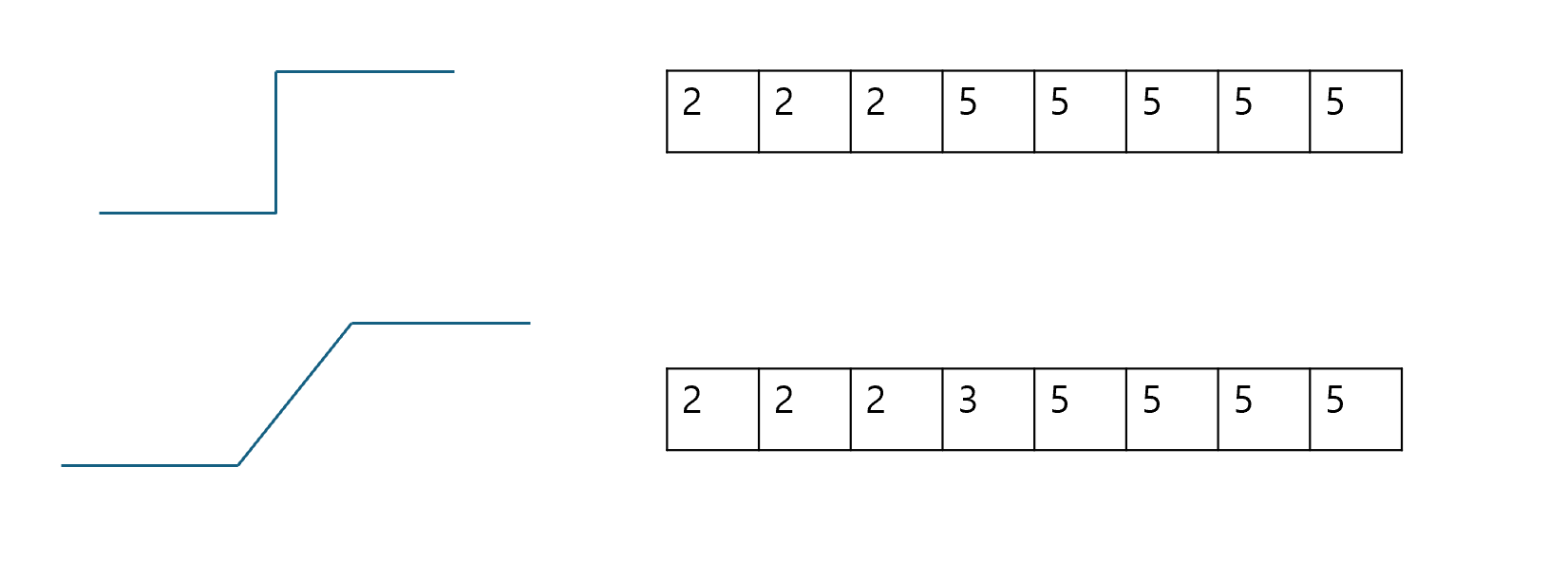
램프 에지는 컨볼루션으로 1차 미분을 하면 정확한 위치를 찾을 수 없다. 하지만, 다행히도 에지가 어떤 방향을 향하는지에 대한 정보는 가지고 있다. (부호)
| 1 | 1 | 1 | 3 | 5 | 5 | 5 | 5 |
| -1 | 1 |
위의 두 개를 컨볼루션 연산을 하면 아래와 같은 값이 된다.
| 0 | 0 | 2 | 2 | 0 | 0 | 0 | - |
1인 부분이 여러개 발생한다.우리는 해당 부분이 어디인지 알 수 없다. 여기서 우리는 한 번 더 미분을 해보는 시도를 할 수 있다.
| 0 | 2 | 0 | -2 | 0 | 0 | - | - |
우리는 이차 미분한 식에서 0교차를 찾을 수 있다. 0교차란 자신은 0이면서 양쪽의 부호가 다른 점이다.
이때, 우리는 미분을 두번 하는 것을 수식적으로 풀어 2차 미분영상의 필터를 새로 구해 한 번만 연산할 수 있다.
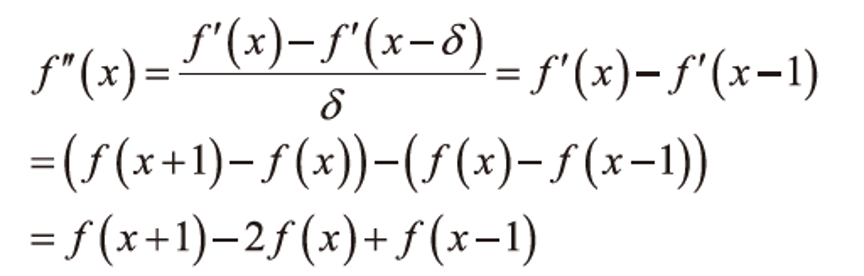
이 과정으로 얻은 필터는 아래와 같다.
| 1 | -2 | 1 |
즉, 에지 검출은 1차 미분에서 봉우리를 찾거나, 2차 미분 영상에서 영교차를 찾는 것으로 정의할 수 있다.
(1) 1차 미분에 기반한 에지 연산자
| -1 | 1 |
위 에지 연산자는 너무 작고 대칭이 아니라서 실제로는 중간에 0을 넣어 확장하여 사용한다.

소벨 연산자는 가까운 상하좌우 화소에 가중치 2를 추가적으로 준다.
그리고 아래 식으로 에지 강도와 에지 강도를 구할 수 있다.

이때 에지 방향은 그레이디언트 방향을 90도 회전한 값이다.
4.2 캐니 에지
Canny는 가장 체게적인 에지 검출 이론으로 인정받는 알고리즘을 제안한다. 최소 오류율, 위치 정확도, 한 두께 라는 기준에 따라 목적 함수를 정의하고 최적화 문제로 풀었다.
이 때, 한 두께 에지를 출력하기 위해 비최대 억제를 적용한다. 비최대 억제란 두 이웃 화소와 비교해 자신이 최대가 아니면 억제된다. 이 때 두 이웃 화소란, 에지 방향에 수직인 화소이다.

캐니 알고리즘은 거짓 긍정을 줄이기 위해 2개의 이력 임곗값 T_low, T_high를 적용한다. 에지는 강도가 T_high 이상인 것부터 진행한다. 이후 추적은 T_low 값을 넘은 값들만 본다. 캐니는 T_high가 T_low의 2~3배가 될 수 있도록 설정하는 것을 권고했다.

여기까지의 모든 알고리즘은 명확한 단점이 있다. 바로, 명암 변화에만 의존한다는 것이다. 따라서 물체 경계에 나타난 에지와 그림자로 인해 발생한 가짜 에지를 구분하지 못한다.
4.3 직선 검출
경계선 찾기
8-연결 에지 화소를 서로 연결해 경계선을 추정할 수 있다. 하지만, 이렇게 하면 짧은 잡읍 경계선이 많이 발생한다.
허프 변환
(1) 허프 변환의 원리
앞에서 경계선이 끊기는 현상을 방지하기 위해 허프 변환을 사용한다. (x,y) 를 지나는 직선은 y = ax + b 로 정의할 수 있다.
한 점을 골라보겠다. (x, y) = (5, 2)
이 점을 y = ax + b 에 대입하고 b에 대한 식으로 정리하면 b = -5x + 2 가 된다.

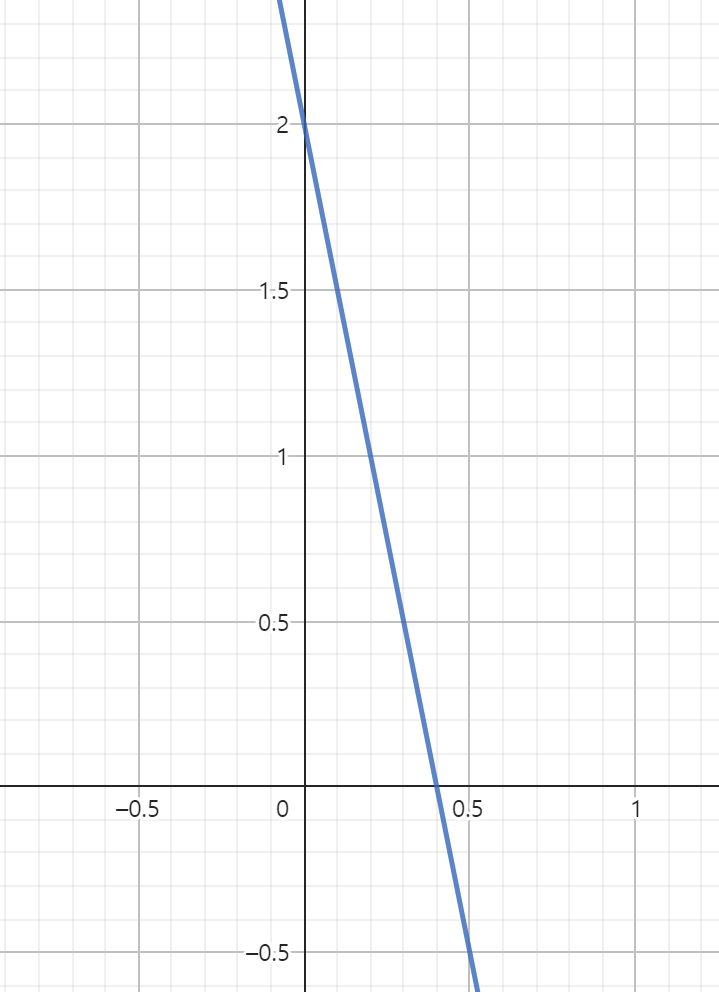
분명 점이었는데 (a,b) 공간으로 변환하면 직선이 된다.
반대로, (a,b) 공간에서 직선이었던 것은 (x,y) 공간에서 점이 된다. 이 원리를 이용하여 아래 과정으로 경계선을 찾을 것이다.
1. 입력한 각각의 점 (x,y) 에 대해 (a,b) 공간에 b = -ax + y 직선을 그린다.
2. 각각의 점이 그려낸 직선이 만나는 점 (a,b)를 찾는다.
3. 찾은 직선을 (x,y) 공간으로 옮긴다. y = ax + b 에서 a,b 값이 결정된 직선이 생긴다.
이 때, 2번 과정에서 만나는 점 (a,b)는 투표로 알아낸다.
(2) 허프 변환의 구현
앞에서의 설명은 허프 변환의 이상적인 상황이다. 우리는 조금 더 실제적인 구현을 위해 몇 가지를 더 고려해야한다.
첫번째, 현실은 여러 개의 많은 점들이 있고, 이 것은 완벽한 일직선을 이루지 못한다. 그래서 a,b 공간을 이산화하여 구간을 나누고 자신이 지나는 모든 칸에 투표를 하여 누적 배열을 만든다.
둘째, 만들어진 누적배열에 잡음이 많다. 그래서 많은 잡음 중 한 점을 결정해야하는데 우리는 여기서 비최대억제를 사용한다. 하지만, 극점만 남긴다고 해도 보통 잡음이 발생하기 때문에 임곗값을 같이 사용한다.
셋째, y = ax+b에서 기울기 a가 무한대인 경우 투표가불가능하다. 이 경우는 극좌표에서 직선의 방정식을 표현하는 식을 도입하여 해결한다.


허프 변환은 방정식은 알려주나, 직선의 양 끝점은 알려주지 못하기 때문에 양 끝점을 알아내려면 비최대 억제 과정에서 극점을 형성한 화소를 찾아 가장 먼 곳에 있는 두 화소를 계산하는 추가적인 과정이 필요하다.

또한, 위의 원의 방정식을 사용하면 원도 검출할 수 있다.
RANSAC
허프만 변환은 모든 점에 같은 투표 기회를 준다. 이 방식의 단점은 누적 배열에 잡음이 매우 심하다면, 아무리 비최대 억제를 사용하더라도 여러 개의 직선을 출력할 수 있을 것이다.
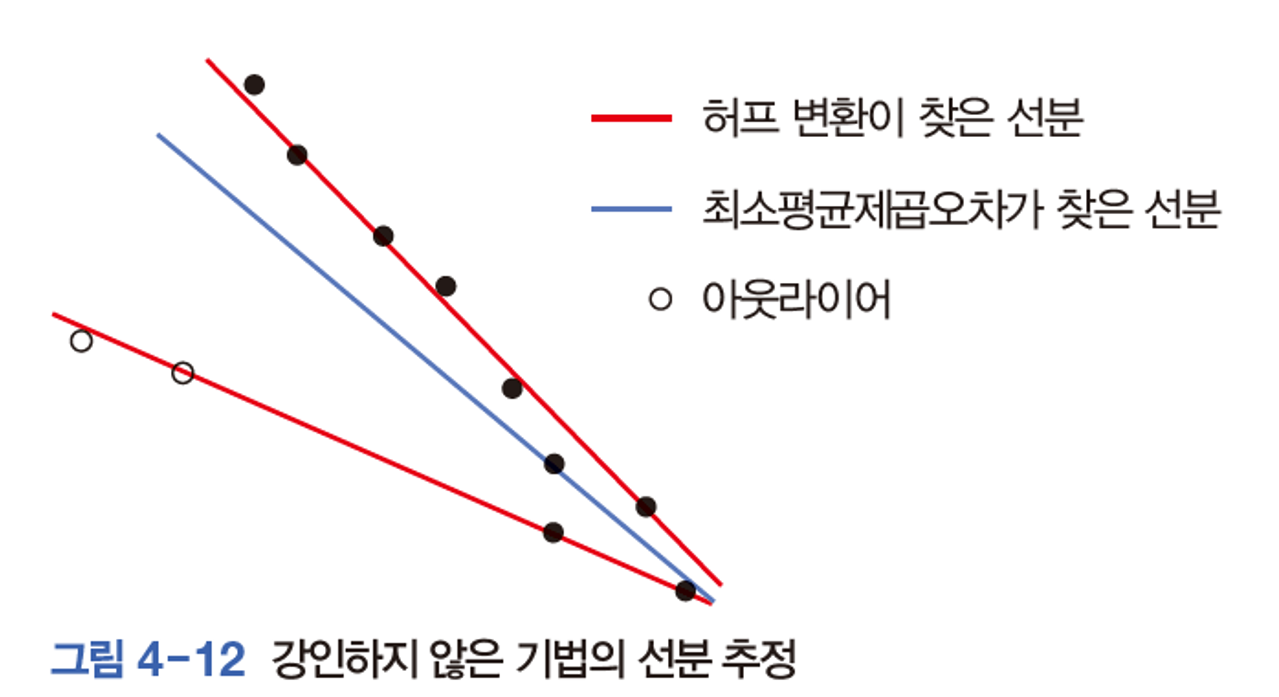
이런 허프변환 같은 방식을 강인하지 않은 기법이라고 한다. 그리고, 아웃라이어를 걸러내는 과정을 가진 추정 기법을 강인한(robust) 추정이라고 한다. robust 한 기법 중 RANSAC이 있다.
RANSAC은 인라이어와 아웃라이어가 섞여있는 상황에서 인라이어를 찾아 최적 근사한다. 과정은 다음과 같다.
1. 랜덤하게 두 점을 선택하고 두 점을 지나는 직선을 계산한다.
2. 일정한 양의 오차 t를 허용해 직선에 일치하는 선의 개수를 센다.
3. 개수가 임계값을 넘지 못하면 가능성이 없다고 보고 버린다.
4. 임계값을 넘은 선을 찾으면, 일치하는 점을 가지고 최적 직선을 추정한다. 그리고 추정 오류를 측정한 뒤 임계값 e보다 작으면 후보군에 추가한다.
5. 후보군 중 최적을 찾아 출력한다.

4.4 영역 분할
배경이 단순한 영상의 영역 분할
배경이 단순한 영상의 영역 분할 방식에는 여러가지가 있다.
1. 오츄 이진화 알고리즘의 확장
오츄 이진화 알고리즘을 여러 임곗값을 활용하도록 확장하면, 영상을 분할할 수 있다.
2. 군집화 알고리즘의 적용
r, g, b 3개 값으로 표현된 화소를 샘플로 보고 3차원 공간에서 클러스터링을 진행한 다음 화소 각각에 클러스터 번호를 부여한다.
3. 워터셰드
비가 오면 오목한 곳에 웅덩이가 생기는 현상을 모방한 연산으로, 에지 강도 맵을 지형으로 간주하여 웅덩이가 생기는 공간을 하나의 영역으로 간주하는 것이다.

슈퍼 화소
슈퍼 화소란 화소 보단 크지만, 물체보다는 작은 영역으로 영상을 슈퍼 화소 단위로 분할 할 수도 있다. 슈퍼 화소 알고리즘은 여러가지가 있으며, SLIC(Simple Linear Iterative Clustering) 에 대해 알아보겠다.
SLIC는 k-means clustering과 유사하게 작동한다.
1. k개 화소를 군집 중심으로 지정함.
이 때, 군집 중심이 물체 경계에 놓이는 일을 방지하기 위해 3x3 이웃에서 그레이디언트가 가장 낮은 화소로 이동한다.
2. 화소 할당
화소 각각에 대해 주위 4개의 군집 중심과 자신까지의 거리를 계산해서 가장 유사한 군집 중심에 할당한다.
3. 평균 계산 및 종료 판단
모든 군집 중심의 이동량의 평균을 구하고, 임계치보다 작으면 수렴했다고 판단하고 알고리즘을 멈춘다.
최적화 분할
이전까지의 알고리즘은 지역적 명암 변화만 살폈다. 하지만, 이렇게만 살펴보면 하나의 물체가 급격하게 색이 변하거나, 배경과 물체의 경계가 뚜렷하지 않은 경우 제대로 된 분할을 할 수 없다. 그래서 전역적인 정보를 추가하여 고려해보고자 한다. 전역적으로 볼 때는 영상으로 그래프로 표현하고 분할을 최적화 문제로 해결한다.
보통 화소 또는 슈퍼 화소를 노드로 취한다. 화소는 매우 많기 때문에 시간 복잡도가 늘어나기 때문에 슈퍼 화소를 이용하여 노드 개수를 줄인다. 두 노드를 연결하는 가중치는 유사도를 이용한다.

정규화 절단 알고리즘
정규화 절단은 화소를 노드로 취한 뒤 f(v) 로 (r,g,v,x,y)를 사용하며, 유사도를 에지 가중치로 사용한다.

cut(C1, C2)는 C1에 포함된 v와 C2에 포함된 c의 유사도의 합이다. 즉, 유사도가 낮을 수록 유사도의 합이 작기 때문에 더 잘 분할되었다고 할 수 있다. 이 cut은 영역 분할의 좋은 정도를 측정해주는 목적 함수로의 역할을 할 수 있다.
하지만, 위 식을 그대로 사용하면 영역을 너무 자잘하게 분할하는 경향이 있기 때문에, 실제로 사용할 때는 정규화를 한다.
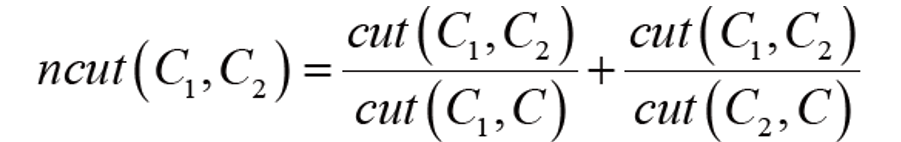
이 알고리즘이 만들어진 10년 뒤 에지 검출과 영역 분할을 결합하고 분할하는 알고리즘을 발표한 뒤 (2011) 이후 별다른 발전이 없는 상황임.
4.5 대화식 분할
분할 알고리즘에 초기 정보를 입력해주는 방식이다.
능동 외곽선
물체 내부에 초기 곡선을 지정하면 곡선을 점점 확장하면서 물체 외곽선으로 접근하는 방식이다. 사용자가 초기 곡선을 지정해주어야하기 때문에 곡선을 표현하는 방법이 필요하다. 이때, 스프라인 곡선 g(l) 을 이용한다.

- e_image : 곡선이 에지에 위치하도록 유지함.
- e_internal : 곡선이 매끄러운 모양이 유지되도록 유도함
- e_domain : 특정 물체의 모양 정보가 잘 유지되도록 유도함. (단, 종종 무시될 때가 있음.)
'Computer Science > AI' 카테고리의 다른 글
| [3DGS] Gaussian function - 1D gaussian (0) | 2025.02.07 |
|---|---|
| [AI] 컴퓨터 비전 - 지역 특징 (모라벡, 해리스, SIFT) (1) | 2024.04.21 |
| [AI] 컴퓨터비전 - 기초 영상 처리 기법 (1) | 2024.04.20 |
| [MIT 6.S191] Convolutional Neural Networks (1) | 2024.02.08 |
| [AI] Ensemble Learning - Voting, Bagging, Boosting, Random Forests (2) | 2023.10.17 |













