[3DGS] gaussian function - N-dim gaussian
Contents
1D gaussian (1편 - 아래 링크 참조)
- gaussian function
- gaussian integral
N-Dim gaussian
- 2D gaussian
- 3D gaussian
2025.02.07 - [Computer Science/AI] - [3DGS] Gaussian function - 1D gaussian
[3DGS] Gaussian function - 1D gaussian
최근 화제가 되고 있는 Gaussian Splatting에 대해 공부하면서 Gaussian에 대한 수학적인 이해가 부족하다는 것을 느꼈다. 본격적으로 관련 분야를 공부하고 싶기 때문에 수식적으로 꼼꼼하게 공부하고
mobuk.tistory.com
N-Dimention gaussian
n차원의 가우시안은 아래와 같이 표현할 수 있다.

이때 C는 positive-definite(모든 eigenvalue가 양수인 square matrix) 행렬이다. C는 실수 행렬인 경우 Symmetric 한 특성을 가지고 있다.
N차 정규분포의 확률밀도함수를 나타내는 식은 아래와 같다

2D gaussian
2D gaussian function의 기본형은 아래 식과 같다.

N차원 가우시안의 형태가 행렬로 표기되어 있어 표기가 잘 와닿지 않았다. 그래서 행렬 표기를 풀어 기본형이 나오는지 직접 계산해보았다. ( 아래 과정은 수학적으로 면밀한 계산이 아니기 때문에 참고만 하길 바란다 )

a = 1, b = 0, c = 1이면 C는 positive-definite matrix가 된다.

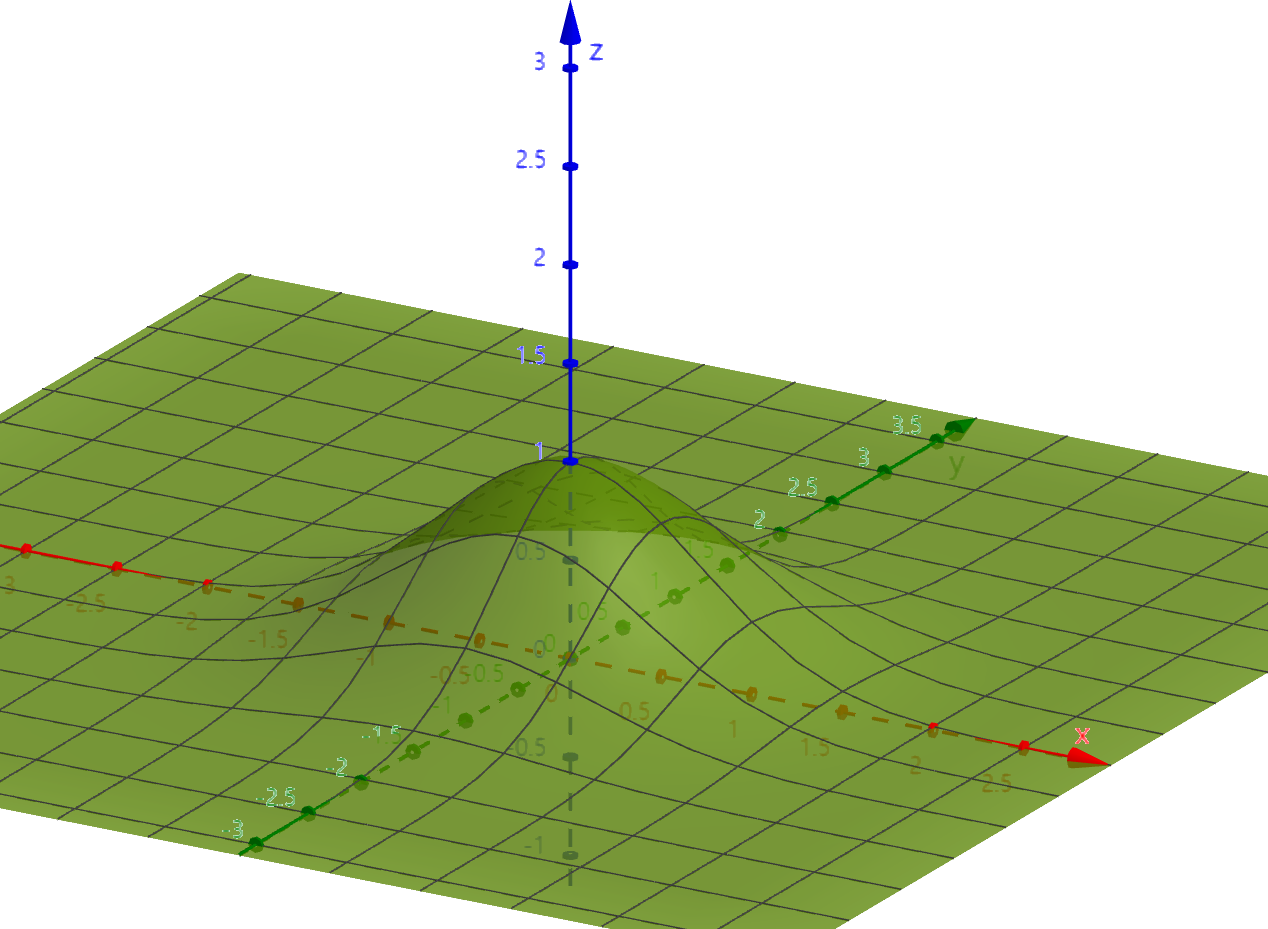
2D 정규분포의 확률밀도함수는 아래 식과 같다.
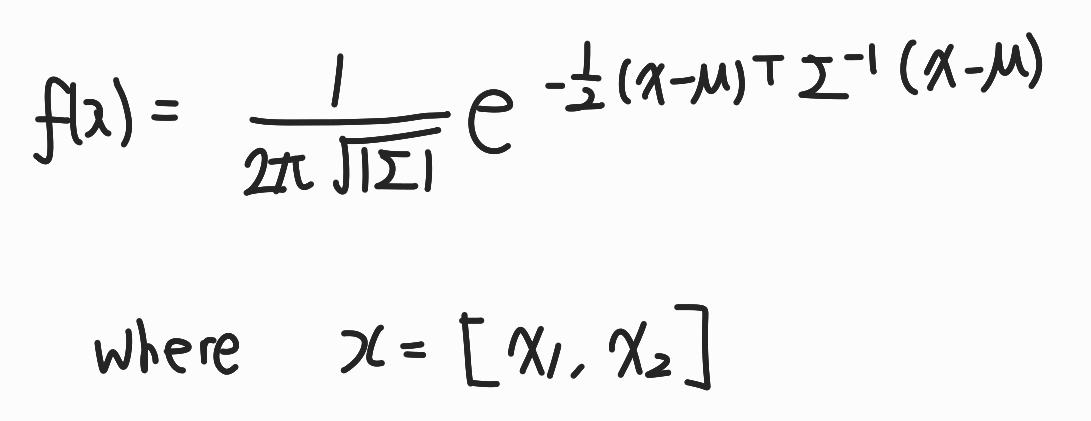
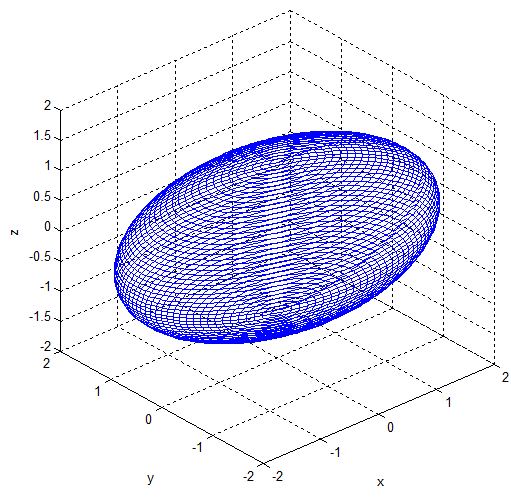
3D gaussian
우리는 N차 가우시안의 식을 알기 때문에 수식적으로는 그냥 2차원 표기를 3차원으로 확장하면 된다. 기하학적으로 3D 가우시안은 ellipsoid의 형태를 띄고 있다.
Gaussian Splatting 논문에서는 3D gaussian 을 사용하며 논문에서 표기한 수식은 아래와 같다.
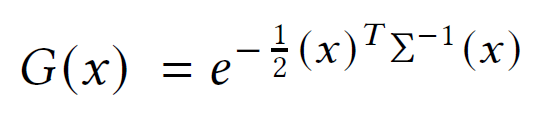
위 가우시안 식에서 µ = 0 이고, 정규화 과정이 필요없기 때문에 정규화하지 않고 있다. 자세한 수식 설명은 논문리뷰할 때 다루도록 하겠다.
3D gaussian이 타원체의 형태를 띄고 있기 때문에 이 것들을 잘 최적화 시켜 물체를 렌더링하는 기술이 3D Gaussian Splatting이라고 할 수 있다.
'Computer Science > AI' 카테고리의 다른 글
| [Nerf] Nerf : Representing Scenes as Neural Radiance Fields for View Synthesis (0) | 2025.03.05 |
|---|---|
| [3DGS] 3D Gaussian Splatting for Real-Time Radiance Field Rendering : Paper Review (0) | 2025.02.11 |
| [3DGS] Gaussian function - 1D gaussian (0) | 2025.02.07 |
| [AI] 컴퓨터 비전 - 지역 특징 (모라벡, 해리스, SIFT) (1) | 2024.04.21 |
| [AI] 컴퓨터 비전 - 영역 분할 (고전적인 기법을 중심으로) (0) | 2024.04.21 |













