[3DGS] 4D Gaussian Splatting for Real-Time Dynamic Scene Rendering

 

Paper Information

• Title : 4D Gaussian Splatting for Real-Time Dynamic Scene Rendering
• Journal : CVPR 2024
• Author : WU, Guanjun, et al.

 

https://guanjunwu.github.io/4dgs/

4D Gaussian Splatting for Real-Time Dynamic Scene Rendering

 

 

Abstract

Purpose : achieve real-time dynamic scene rendering

Main Method : 4D Gaussian Splatting

How : 

• novel explicit representation containing both 3D Gaussian and 4D neural voxels
• decomposed neural voxel encoding algorithm
• lightweight MLP

Result : achieves real-time rendering under high resolutions

 

1. Introduction

Novel view synthesis (NVS) : render images from any desired viewpoint or timestamp of a scene

NeRF : represents scenes with implicit functions
However, the original NeRF method bears big training & rendering costs

3D-GS : focuses on the static scenes
(Extending 3D-GS to dynamic scenes is difficult)

goal : constructs a compact representation 

contributions : 

• efficient 4D Gaussian splatting framework
• multi-resolution encoding method
• real-time rendering on dynamic scenes

 

2. Related Works

 

2.1. Novel View Synthesis

Much approaches are proposed to represent a 3D object and render novel views

Representations : light field, mesh, voxels, multi-planes

NeRF-based approaches :demonstrate implicit radiance fields 
=> accelerates the learning time for dynamic scenes to half an hour

Flow-based methods :
1) adopt warping algorithm to SNV by blending nearby frames
2) adopt decomposed neural voxels (further advancements)
3) treat sampled points in each timestamp individually
=> fast, but dynamic scene X

Our methods:
aims at constructing a highly efficient training and rendering pipeline while maintainting the quality, even for sparse inputs

 

2.2 Neural Rendering with Point Clouds

Point-cloud-based methods : initially target 3D segmentation and classification
combines approaches for volume rendering => achieving rapid convergence speed for dynamic novel view synthesis.

3D-GS : pure explicit representation and differential point-based splatting methods

Dynamic3DGS : models dynamic scenes by tracking the position and variance of each 3D Gaussian at each timestamp

• memory consumption : O(tN) N // # of 3D Gaussians => storage cost ↑ 

Our approach (4DGS)

• memory consumption : O(N + F) // F : parameters of Gaussians deformation fields network
• With compact network, results in highly efficient training efficiency and real-time rendering

 

 

3. Preliminary

3.1. 3D Gaussian Splatting

: explicit 3D Scene representation in the form of point clouds

Eq.1. Gaussian

 

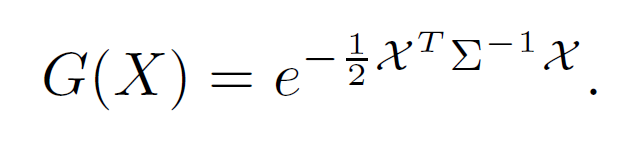
covariance matrix ∑ (world space)
(R = Rotation matrix, S : Scaling matrix)

 

For rendering, We have to project 3D onto 2D.

covariance matrix  ∑' (camera space)
(W = viewing transform matrix, J = Jacobian matrix of the affine approximation of the projective transformation)

 

summary

each gaussian is characterized by the following attributes

• position : X ∈ R3
• spherical harmonic coefficients  : C ∈ Rk
• opacity : α ∈ R
• scaling factor : s ∈ R3
• rotation factor : r ∈ R4

All above the values are computed using Gaussian's representation Eq.1

+) For more information about 3D-GS, please refer to the link below

2025.02.11 - [Computer Science/AI] - [3DGS] 3D Gaussian Splatting for Real-Time Radiance Field Rendering : Paper Review

[3DGS] 3D Gaussian Splatting for Real-Time Radiance Field Rendering : Paper Review

 

 

3.2. Dynamic NeRFs with Deformation Fields

All the dynamic NeRF algorithms can be formulated as : 

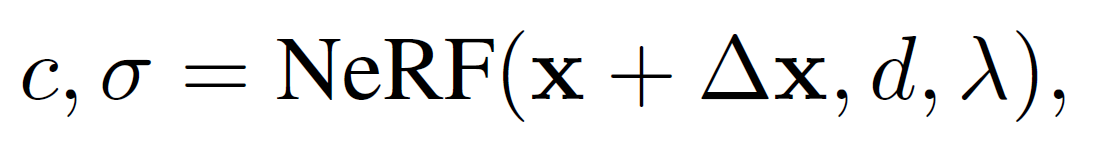
• M is a mapping 8D space(x, d, t, λ) to 4D space (c, σ)
• λ : optional input
• d : stands for view-dependency

world-to-canonical mapping : 

canonical-to-world mapping : 

For more information about NeRF, please refer to the link below.

2025.03.05 - [Computer Science/AI] - [Nerf] Nerf : Representing Scenes as Neural Radiance Fields for View Synthesis

[Nerf] Nerf : Representing Scenes as Neural Radiance Fields for View Synthesis

 

4. Method

4.1. 4D Gaussian Splatting Framework

• view matrix :  M = [R, T] 
• timestamp : t
• ˆI : novel-view image (rendered by differential splatting)

ˆI = S(M, G′), where G′ = ΔG + G.

• ΔG : deformation of 3D Gaussians 
  => ΔG = F(G, t) // F : deformation field network
  => ΔG = D(f),  fd = H(G, t),
• G' : deformed 3D Gaussians
• G : original 3D Gaussians

 

4.2. Gaussian Deformation Field Network

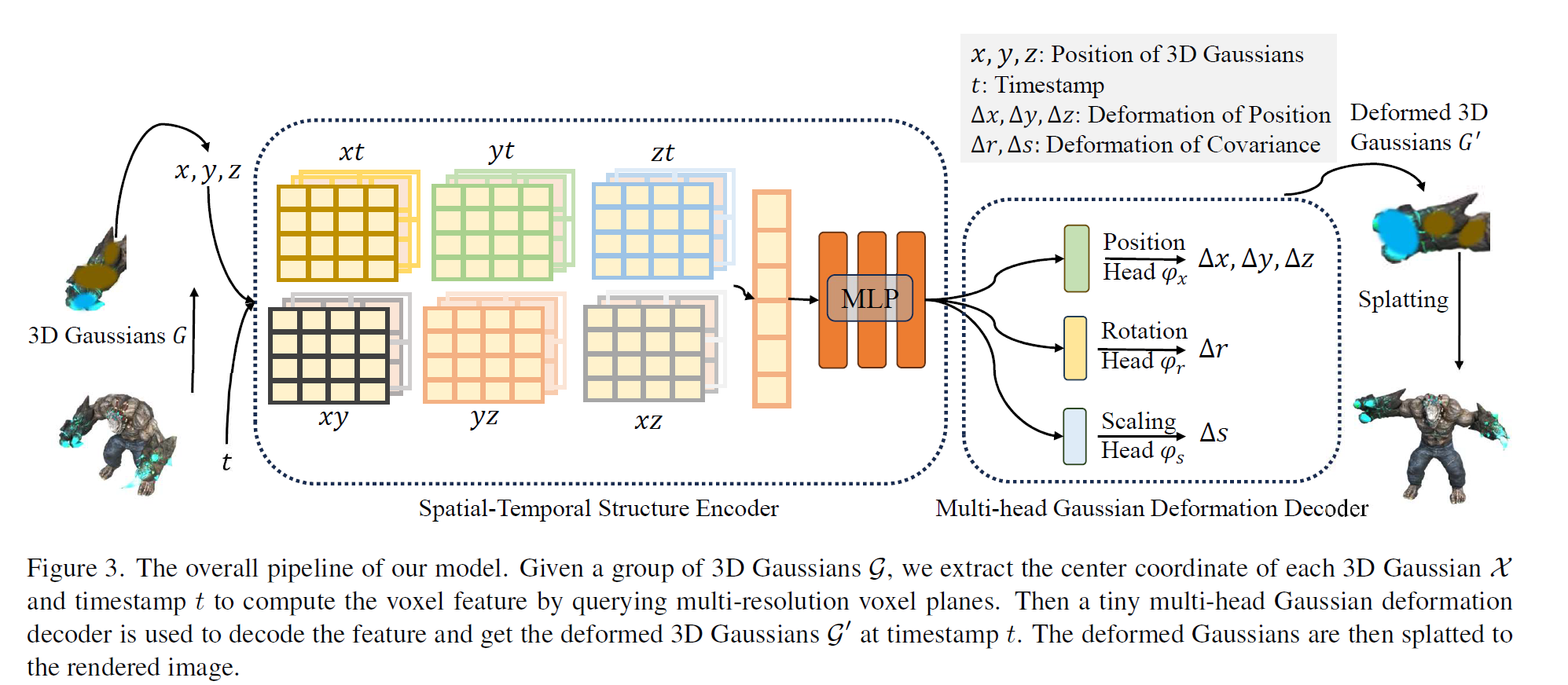
Spatial-Temporal Structure Encoder

H : spatial-temporal structure encoder including a multi-resolution HexPlane R(i, j)
=> 6 plane modules Rl(i, j)

H(G, t) = {Rl(i, j), ϕd | (i, j) ∈ {(x, y), (x, z), (y, z), (x, t), (y, t), (z, t)}, l ∈ {1, 2}}.

• tiny MLP ϕd 
• R(i, j) ∈ Rh×lNi×lNj
• N : basic resolution of voxel grid
• l : upsampling scale

interp : bilinear interpolation

fd = ϕd(fh).

Multi-head Gaussian Deformation Decoder 

D : multi-head gaussian decoder

D = {ϕx, ϕr, ϕs}

• deformation of position : ΔX =ϕx(fd)
• rotation : Δr = ϕr(fd),
• scaling : Δs = ϕs(fd).

Finally we obtained the deformed 3D Gaussians G' = {X′, s′, r′, σ, C}.

 

4.3. Optimization 

3D Gaussian Initialization

fine-tuned in proper 3D Gaussian initialization => initial 3000 iterations , render images with 3D Gaussian I = S(M, G).

 

Loss Function

L1 color loss, L_tv : grid-based total-variational loss

 

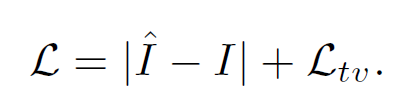
5. Experiment

• implimentation : Pytorch
• gpu : RTX 3090

5.1. Experimental Settings

Synthetic Dataset

Datasets introduced by D-NeRF

https://github.com/albertpumarola/D-NeRF

GitHub - albertpumarola/D-NeRF

 

Real-world Dataset

Datasets provided by HyperNeRF, Neu3D

https://github.com/google/hypernerf

GitHub - google/hypernerf: Code for "HyperNeRF: A Higher-Dimensional Representation for Topologically Varying Neural Radiance Fi

 

https://github.com/facebookresearch/Neural_3D_Video

GitHub - facebookresearch/Neural_3D_Video: The repository for CVPR 2022 Paper "Neural 3D Video Synthesis"

 

5.2. Results

evalutation metrics : PSNR, SSIM, LPIPS, MS-SSIM, FPS, D-SSIM

qualtiy of novel view synthesis(Tab. 1.)

• high rendering quality within the synthesis dataset
• fast rendering speeds while keeping low storage consumption 

 

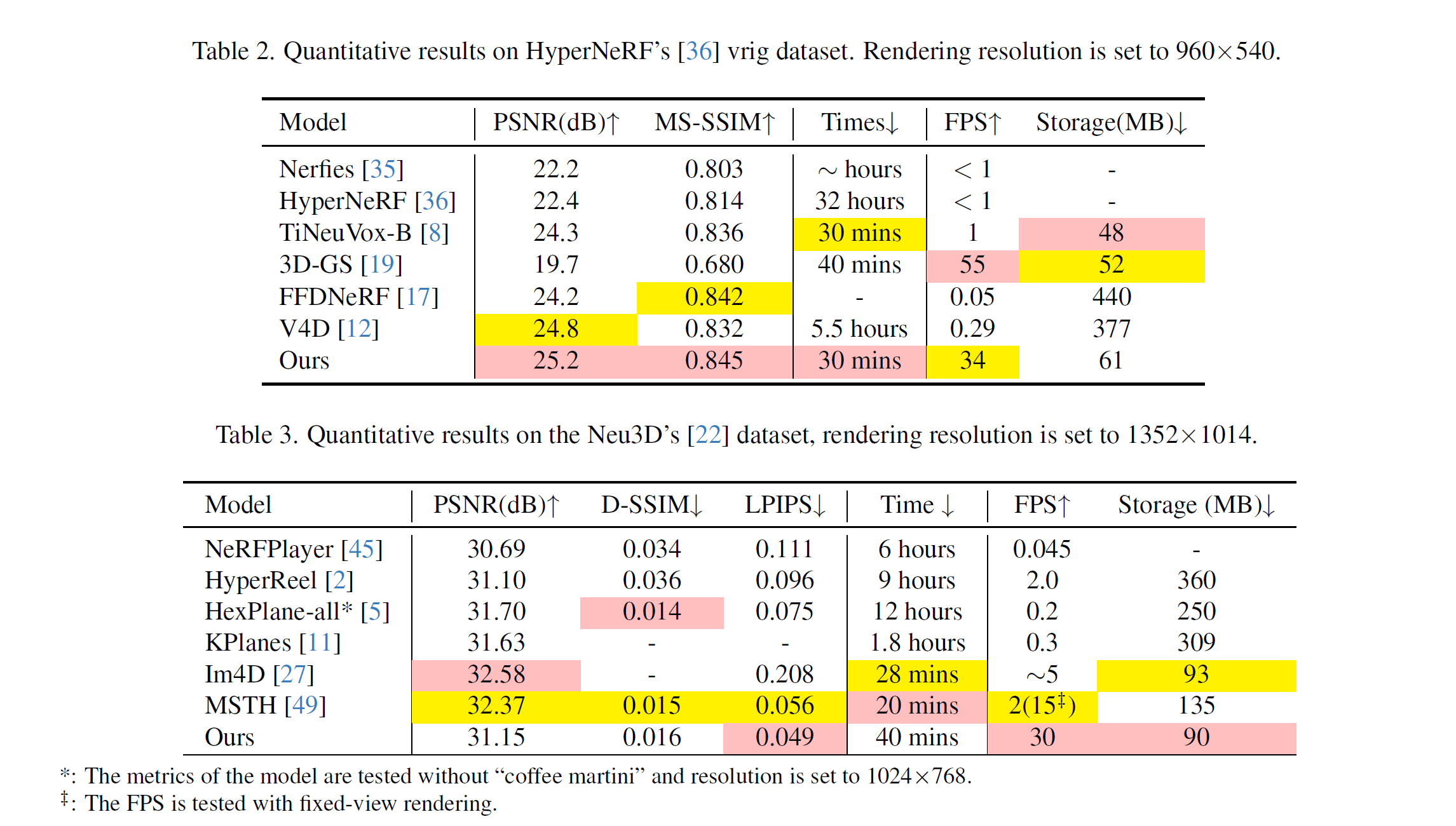
Real-word datasets (Tab. 2. / Tab. 3.)

• comparable rendering quality
• fast convergence
• excel in free-view rendering speed in indoor case

However, multi-cam setups need to improve. 

 

5.3. Ablation Study

• Spatial-Temporal Structure Encoder
• Gaussian Deformation Decoder
• 3D Gaussian Initialization 

 

5.4. Discussions

 

Tracking with 3D Gaussians

This methods : can present tracking object in monocular settings with pretty low storage

 

Composition with 4D Gaussians

 

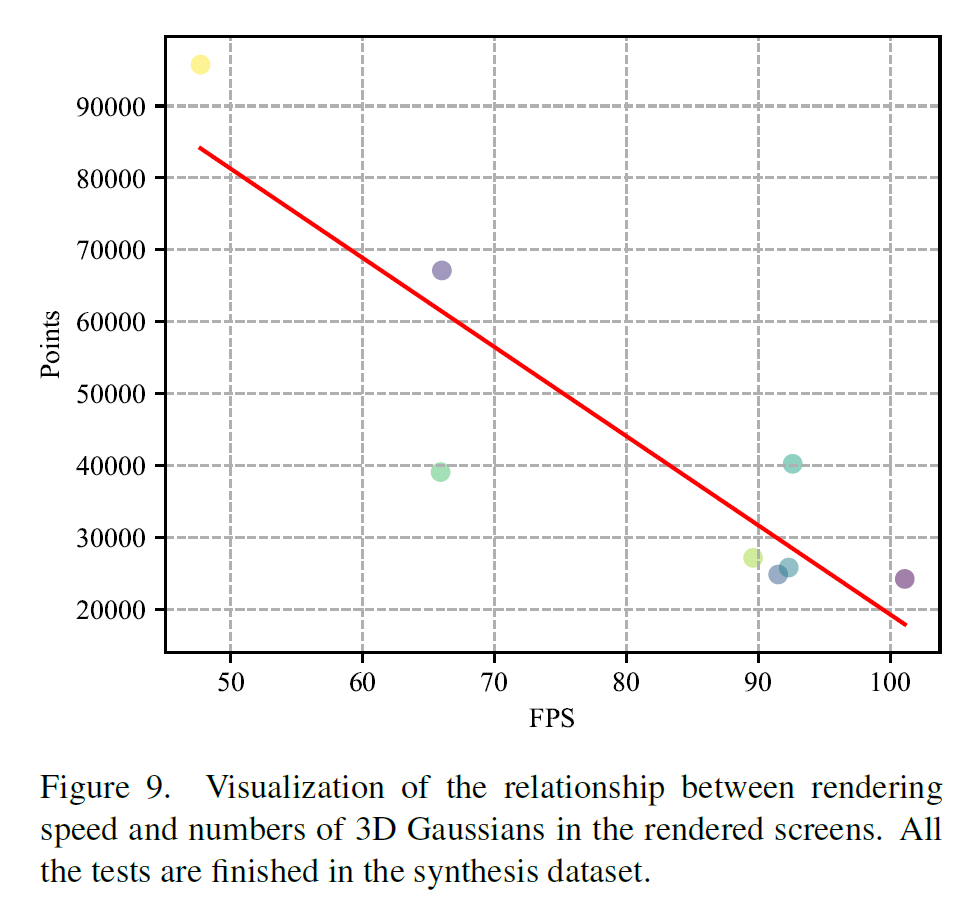
Analysis of Rendering Speed

5.5. Limitation

1. weakness in large motions, absense of background points, unprecise camera pose 
2. not split the joint motion of static and dynamic Gaussian parts under the monocular settings without any additional supervision
3. more compact algorithm needs to be designed to handel urban-scale reconstruction

 

6. Conclusion 

This paper proposes 4D Gaussian splatting to achieve real-time dynamic scene rendering

• efficient deformation field network
• adjacent Gaussians connected via a spatial-temporal structure encoder
• connection between Gaussians lead to more complete deformed geometry

=> can model dynamic scenes + have the potential for 4D objective tracking & editing