[3DGS] Scaffold-GS : Structured 3D Gaussians for View-Adaptive Rendering

 

Paper Information

• Title : Scaffold-GS : Structured 3D Gaussians for View-Adaptive Rendering
• Journal : CVPR 2024
• Author : Lu, Tao, et al.

 

 

https://city-super.github.io/scaffold-gs/

Scaffold-GS: Structured 3D Gaussians for View-Adaptive Rendering

 

 

Abstract

problems : 3D Gaussian Splatting method often leads to heavily redundant gaussians

main method : Scaffold-GS

details : 

• uses anchor points
• predicts their attributes on-the-fly

results : 

• effectively reduces redundant Gaussians while delivering high-quality rendering
• demonstrates an enhanced capability to accommodate scenes with varying levels-of-details and view-dependent observations.

 

1. Introduction

Traditional primitive-based representation (meshes and points)
 : discontinuity &  blurry artifacts

volumetric represenations and neural radiance field(NeRF)
 : high cost of time-consuming stochastic sampling

3D Gaussian Splatting (SOTA)
 : excessively expand Gaussian balls to accommodate every training view => significant redundancy

 

Therefore, we present Scaffold-GS, a Gaussian-based approach that utilizes anchor point

• construct a sparse grid of anchor points initiated from SfM points
• develop 3D Gaussians through growing and pruning operations

As a result, this approach can render at a similar speed as the original 3D-GS with little computational overhead

 

Summary

1. uses anchor points
2. predicts neural Gaussians from each anchor on-the-fly
3. develops a more reliable anchor growing and pruning strategy

 

 

2. Related Work

MLP-based Neural Fields and Rendering

Early neural fields typically adopt a multi-layer perceptron as the global approximator of 3D scene geometry and appearance

• major challenge = "speed"
  : need to be evaluated on a large number of sampled points along each camear ray.

 

Grid-based Neural Fields and Rendering

This scene representations are usually based on a dense uniform grid of voxels

• major challenge = "speed"
  : still need to query many samples to render a pixel & struggle to represent empty space

 

Point-based Neural Fields and Rendering

Point-based representations utilize the geometric primitive(point clouds) for scene rendering

• major challenge = "discontinuity"
  => Point-NeRF : utilize 3D volume rendering ( hard to volumetric ray-marching)
  => 3D-GS : employ anisotropic 3D Gaussians = real-time

 

3. Method

3.1. Preliminaries

2025.02.11 - [Computer Science/AI] - [3DGS] 3D Gaussian Splatting for Real-Time Radiance Field Rendering : Paper Review

[3DGS] 3D Gaussian Splatting for Real-Time Radiance Field Rendering : Paper Review

 

3.2. Scaffold-GS

 

3.2.1 Anchor Point Initialization

Use sparse point cloud from COLMAP

• V ∈ R^N×3
• ⌊ . ⌉ : rounding operation
• { . } : removing duplicate entries

=> can reduce the redndancy and irregularity in P

 

further enhance f_v to be multi-resoluation and view-dependent

1) creates a features bank : {f_v, f_v↓1, f_v↓2}  // ↓n : down-sampled by 2^n factors

2) blends the feature bank with view-dependent weights to form an integrated anchor feature

 

 

3.2.2 Neural Gaussian Derivation

how derives neural Gaussians from anchor points

 

parameter of neural Gaussian

• position µ ∈ R 3 ,
• opacity ³ ∈ R,
• covariance-related quaternion q ∈ R 4
• scaling s ∈ R 3
• color c ∈ R 3

 

calculation of Gaussians' position

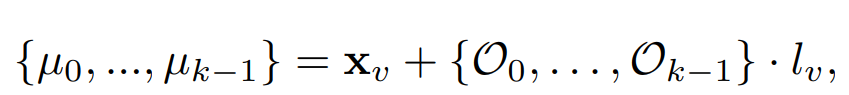
• {μ0, μ 1, ..., μk−1} : position of Gaussian
• Xv : anchor point
• {O0, O1, ..., Ok−1} ∈ R k×3 : the learnable offsets 
• lv : the scaling factor
• k : decoded from the anchor feature

 

calculation of Gaussians' attribute 

Through individual MLP, we can derive Fα(opacity), Fc(color), Fq(quaternion), Fs(scale)

 

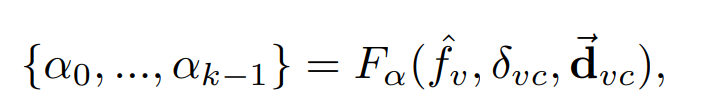
how cuts down computational load

• "on-the-fly" : only anchors visible within the frustum activated to spawn neural Guassians
• keep Gaussians only opcaity value > threshold τα

 

 

3.3 Anchor Point Refinement

growing operation

error-based anchor groing policy : grows new anchors where neural Gaussians find significant

significant : ∇g > τg    (where ∇g is averaged gradients) 

If voxels are deened as significant, new anchor point is deployed

where m denotes the level of quantization

 

+) random elimination => prohibit rapid expansion of anchors

 

pruning operation

To eliminate trivial anchors, accumulate the opacity values of their associated neural Gaussians over N training iterations

=> If an anchor fails to produce neural Gaussians with a satisfactory level of opacity, we then remove it from the scene.

 

observation threshold

To enhance the robustness of Growning and Pruning operations, implement a mininum observation threshold for anchor refinement control.

 

3.4 Losses Design

 

 

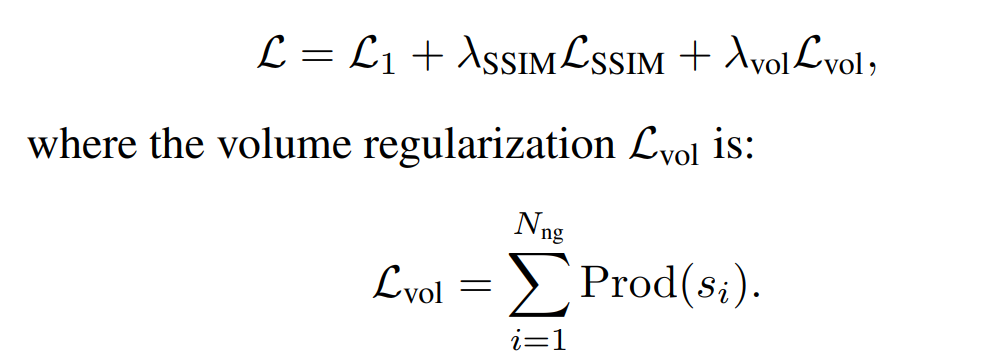
4. Experiments

4.1. Experimental Setup

Dataset and Metrics

1. Dataset

all available scenes tested in 3D-GS

• 9 from Mip-NeRF360
• 2 from Tanks&Temples
• 2 from DeepBlending and synthetic Blender dataset

evaluated on datasets with contents captured at multiple LODs

• 6 from BungeeNeRF
• 2 from VR-NeRF

2. Metrics

• PSNR
• SSIM
• LPIPS
• MB
• FPS

Baseline and Implementation

3D-GS : selected as our main baseliine for its esablished SOTA performance (trained for 30k iterations)

+) k = 10,
MLP = 2-Layer MLPs(with ReLU, hidden 32), gradient average every 100 iter, 
τg = 64ε, rg  = 0.4, rp = 0.8
λ_SSIM = 0.2, λ_vol = 0.001

 

4.2. Result Analysis

 

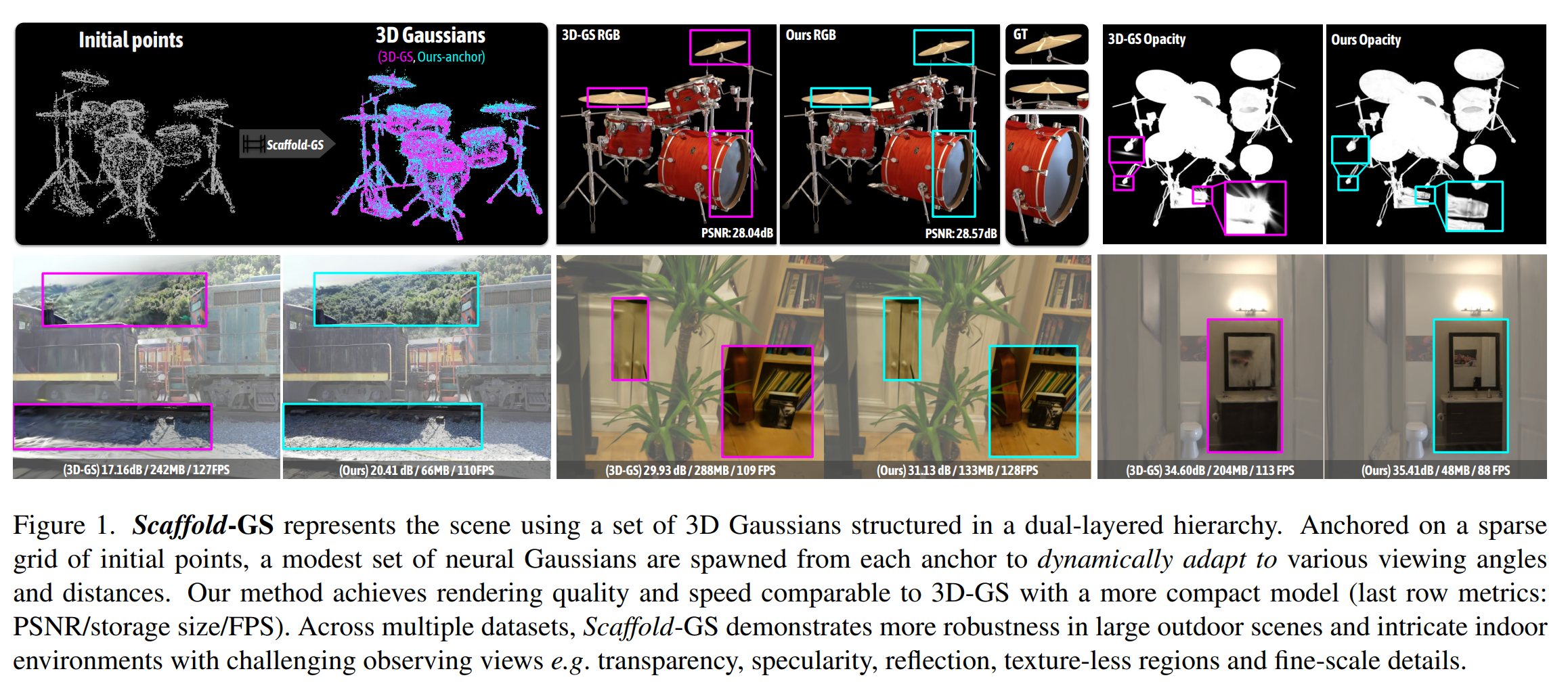
Comparisons

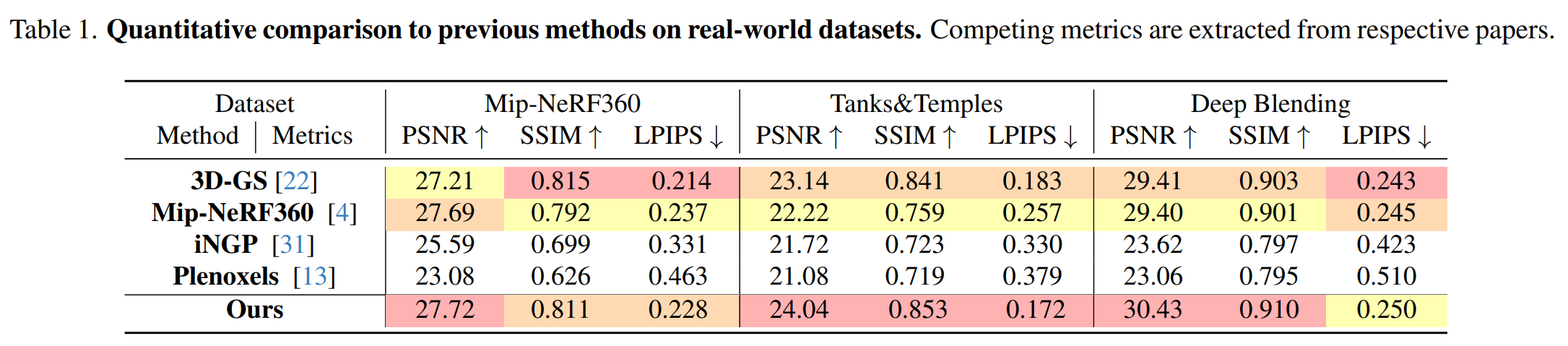
real-world datasets
: Scaffold-GS achieves comparable results with the SOTA algorithms on Mip-NeRF 360 dataset
and surpasses the SOTA on others

efficiency
: achieves real-time rendering while using less storage
and converge faster then 3D-GS

synthetic Blender dataset
: achieve better visuall quality with more reliable geometry and texture details

 

Multi-scale Scene Contents

capability handling multi-scale scene details
: efficiently encoded local structures into compact neural features

 

Feature Analysis

 

View Adaptability

 

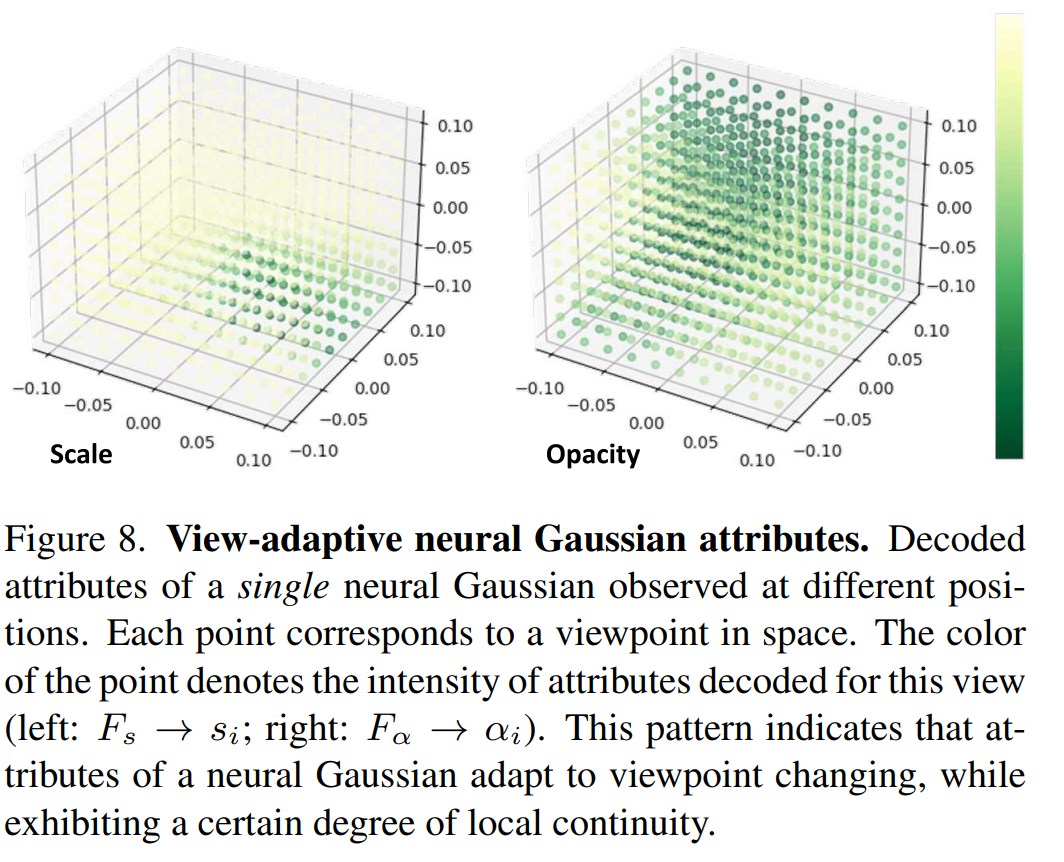
4.3. Ablation Studies

Efficacy of Filtering Strategies

 

Efficacy of Anchor Points Refinement Policy

 

4.4 Discussions and Limitations

• high dependency of initial points
• initializing from SfM point clouds may be suboptimal for scenarios
• suffering from extremely sparse points (despite of anchor point refinement...)

 

5. Conclusion

In this work, we introduce Scaffold -GS, a novel 3D neural scene representation for efficient view-adaptive rendering

• 3D Gaussians guided by anchor points from SfM
• attributes are on-the-fly decoded from view-dependent MLPs

=> leverages a much more compact set of Gaussians to achieve comparable or even better results than the SOTA algorithm

"view-adaptive" : particularly evident in challenging cases where 3D-GS usually fails