- Title : Compressed 3D Gaussian Splatting for Accelerated Novel View Synthesis
- Author : Niedermayr, Simon, Josef Stumpfegger, and Rüdiger Westermann.
- Journal : CVPR 2024

https://keksboter.github.io/c3dgs/
Compressed 3D Gaussian Splatting for Accelerated Novel View Synthesis
Ours 21 MB 3DGS 600 MB Ours 22 MB 3DGS 602 MB
keksboter.github.io
Abstract
problem : 3DGS - hard to use
method : Compressed 3D Gaussian Spatting
details:
- sensitivity-aware vector clustering => Color, Gaussian
- quantization-aware fiine-tuning
- entropy encoding
results: achieve a compression rate of upp to 31x on real world
Introduction
Novel View Synthesis
- NeRF : expensive neural network evaluations
- explicit scene scene representation (such as voxel) : needed multresolution hash encoding for real-time
However, current method requires exhaustive memory resources
=> dedicated compression scheme to overcome these limitations
differentiable 3D Gaussian Splatting : consist of millions of Gaussians and require up to several gigabytes of storage and memory
=> We suggest compressed 3DGS and reduces the storage requirements of typical scenes by up to a factor of 31x.
three main step
- sensitivity-aware clustering
- quantization-aware fine-tuning
- entropy encoding
+) we propose a renderer for the compressed scene
2. Related Work
Novel View Synthesis
NeRF(Neural Radiance Fields) : use neural networks to model a 3D scene
=> slow, high memory
many different scene models to speed up training and rendering efficiency
- structured space discretizations (voxel grid, octree, hash grid)
- point-based repreesntations to avoid empty space
- differentiable splatting
=> 3D Gaussian Splatting achieves SOTA performance
NeRF Compression
- tensor decomposition
- frequency domain transformation
- voxel pruning
- vector quantization : compress grid-based radiance fields by up to a factor of 100x
- hash encoding with vector quantization : reduces required memory
Many works have addressed memory reduction during inference
Our approach is the first aims at the compression of point-based radiance fields to enable high-quality novel view synthesis
Quantization-Aware Training
weight quantization : reduces quantization errors
=> usages : neural scene representations, voxel-based NeRFs
Various approaches for weight quantization have been explored to reduce size and latency
=> rely on the observation that in most cases lower precision is required for model inference than for training
- post-training quantization : model weights are reduced to a lower bit representation after training
- quantization-aware training : full precision to obtain numerically stable gradients
3. Differentiable Gaussian Splatting
final scene representation : a set of 3D Gaussians
- covariance matrix ∑ ∈ R^3x3 : parameterized by R, S
- 2d projection covariance matrix ∑' = JW ∑W^TJ^T
- pixel's color C
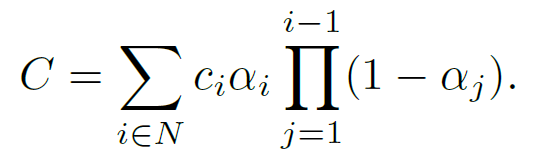
position x, rotation q, scaling s, opacity a, SH coeffients of each 3D Gaussian are optimized.
For more details, please refer below link
[3DGS] 3D Gaussian Splatting for Real-Time Radiance Field Rendering : Paper Review
Paper InformationSIGGRAPH 2023title : 3D Gaussian Splatting for Real-Time Radiance Field Rendering journal : ACM Transactions on Graphicsauthor : Kerbl, Bernhard and Kopanas, Georgios and Leimkhler, Thomas and Drettakis, Georgehttps://rep
mobuk.tistory.com
4. Sensitivity-Aware Scene Compression
- sensitivity-aware vector clustering
- quantization-aware fine-tuning
- Sorting, Entropy & Run Length Encoding

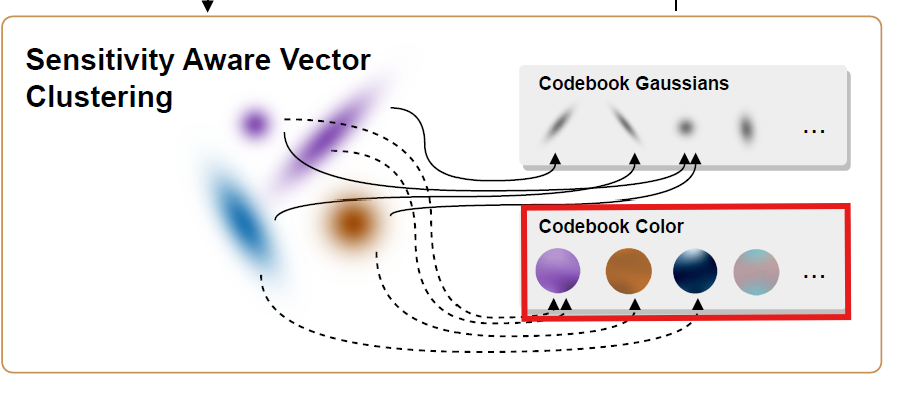
4.1. Sensitivity-Aware Vector Clustering
This paper utilize vector clustering for compressing 3D Gaussian kernels
=> encode SH coefficients and Gaussian shape features into two seperate codebooks(scale, rotation)
Parameter Sensitivity
The sensitivity of the reconstrution quality : not consistent. -> slight cange in one parameter of a Gaussian can cause a significant difference
=> define the sensitivity S of image quality to changes in paremeter p
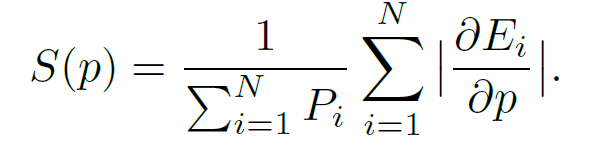
- N : # of images
- Pi : # of pixels in image i
- E : total image energy ( sum of RGB components )
With this formulation, the sensitivity to every parameter can be computed with a single backward pass over each of the training training images.
Sensitivity-aware k-Means
Define sensitivity of vector x as the maximum over its component's sensitivity

Then, the sensitivity measure used for sensitivity-aware clustering to compute codebooks C.
A codebook is obtained by using k-Means clustering with D as a similarity measure.
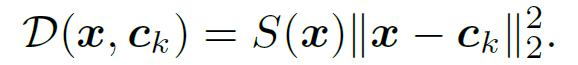
k-Means algorithm for c3dgs:
1) The codebooks are initialized randomly with a uniform distribution.
2) the centroids are computed with an iterative update strategy.
In each steps :
- pairwise weighted distances are calculated
- centroid which has the minimum distance assign
3) each centroid is then updated as

- A(k) : set of vectors assigned to centroid ck
- For performance reasons, a batched clustering strategy is used
In each update steps: centroids are updated usign the moving average with a decay factor λd.
Color Compression
Each Gaussian stores SH coefficients and this paper treat SH coefficients as vectors & compress them into a codebook
Only SH coefficients of a tiny fraction of all Gaussians affect image quality

For small percentage of all SH coefficients ( < 5% ), the sensitivity measure indicates a high sensitivity towards the image quality.
=> Do not consider SH vectors with a sensitivity higher than a threshold βc in the clustering process
Gaussian Shape Compression

3D Gaussian kernel can be parameterized with R and S. Clustering is performed using the normalized covariance matrices. Each Gaussian, a codebook index and scalar scaling factor η stored

Do not consider SH vectors with a sensitivity higher than a threshold βg in the clustering process
+) Due to floating point errors, clustering can lead to non-unit scaling vectors => re-normalized each codebook after each update step.
After clustering, each codebook entry is decomposed into a rotation and scale parameter using an eigenvalue decomposition. (required for quantization-aware training)
In the final codebook, each matrix's R and S are encoded via 4 (quarternion) plus 3 (Scaling) scalar values.
=> we observe up to 15% splats do not impact training images (zero sensitivity => prune)
4.2. Quantization-Aware Fine-Tuning
The parameter can be fine-tuned to regain lost information after compression. For two codebooks, the incoming gradients for each entry are accumulated and then used to update the codebook parameters.
For fine-tuning, we utilize quantization-aware training with Min-Max quantization to represent the scene parameters with fewer bits.
Forward pass :
quantization of a parameter p is simulated using a rounding operation considering the number of bits
and the moving average of each parameter’s minimum and maximum values.
Backward pass :
ignores the simulated quantization and calculates the gradient w.r.t. p as without quantization
[Opacity]
Sigmoid function => Opacity quantization
[Scaling & Rotation]
quantization of scaling and rotation vector => normalization => activation function
We quantize all Guassian parameters without position to 8-bit representation, and position uses 16 bit float quantization.
4.3. Entropy Encoding
After quantization-aware fine-tuning, the compressed scene representation consists of a set of Gaussian and the codebooks
The data then compressed using DEFLATE compression algorithm
Reconstructed scene have spacially coherent features such as color, scaling factor and position. Therefore, we ordered them using Morton order and placed them along a Z-order curve
+) Additionally, the codebook indices were further compressed to fit within the size of the codebook.
5. Novel View Rendering
Preprocess
- Gaussians whose 99% confidence interval does not intersect the view frustum after projection are discarded
- Color, opacity, projected screen-space position, covariacne values stored in an atomic linear-append buffer
- We use the Onesweep sorting algorithm by Adinets and Merrill
Rendering
- Gaussians are finally rendered in sorted order via GPU rasterization.
- A vertex shader computes the screen space vertex positions of each splat from the 2D covariance information
- The pixel shader then discards fragments outside the 99% confidence interval
=> All remaining fragments use their distance to the splat center to compute the exponential color and opacity falloff and blend their final colors into the framebuffer.
6. Experiments
6.1. Datasets
Mip-Nerf360, Tanks&Temples, Deep Blending, NeRF-Synthetic
6.2. Implementation Details
- decay factor λd = 0.8
- batch size : 2^18
- default codebook size : 4096
- βc = 6*10^-7, βg = 3*10^-6
- optimization steps : 5000
6.3. Results
metrics : PSNR, SSIM, LPIPS



Image Quality Loss

Compression Runtime
compression process takes about 5-6 mintues and increases the reconstruction time by roughly 10%
Rendering Times
increase of up to a factor of 4x in rendering speed

6.4. Ablation Study
Loss Contribution & Codebook Sizes

Sensitivity Thresholds

6.5. Limitations
The current inability to aggressively compress the Gaussians' positions in 3D space
7. Conclusion
novel compression and rendering pipeline for 3D Gaussians with color and shape parameters, achieving compression rates of up to 13x and up to a 4x increase in rendering speed.
In the future, we aim to explore new approaches for reducing the memory footprint during the training phase, and additionally compressing positional information end-to-end
'Computer Science > AI' 카테고리의 다른 글
| [Video Compression] Plug-and-Play Versatile Compressed Video Enhancement (1) | 2025.09.12 |
|---|---|
| 3DGS를 위한 COLMAP-GUI 사용법 (1) | 2025.05.09 |
| [3DGS] LightGaussian: Unbounded 3D Gaussian Compression with 15x Reduction and 200+ FPS (0) | 2025.04.21 |
| [3DGS] Text-to-3D using Gaussian Splatting / ver. Kor (0) | 2025.04.07 |
| [3DGS] Mip-Splatting: Alias-free 3D Gaussian Splatting / Ver.Kor (0) | 2025.03.31 |













